関数 関数y =ax2(2) 1 次の各問いに答えなさい。 (1)yはxの2乗に比例し、x=3のときy =27である。 ① yをxの式で表しなさい。 ② x=5のときのyの値を求めなさい。 (2)関数y =ax2で,x=2のときy =−8である。 ① aの値を求めなさい。 ② x=−4のときのyの値を求めなさい。 (3)yはxの2乗に比例し,x=−2のときy =−4・ yはxの2乗に比例する関数,y=ax 2 となるものがある。 ③ 本時の振り返りをワークシートに記述する。 本時の内容をまとめることができるように,調べた関数が,比例,反比例,一次関数ではない根拠を個人でワークシートに記述する場を設定する。<関数y=ax2 に関する変更点> ・目標では、「いろいろな関数」が「関数」へと変更され、それに伴って内容から「2乗に反比例」のグ ラフが無くなった。 ・内容で「集合と関数」・「定義域と値域」が無くなった。 平成元年→平成10 年
中学数学 Y Ax 2 図形との融合問題 中学数学の無料オンライン学習サイトchu Su
関数y=ax2乗
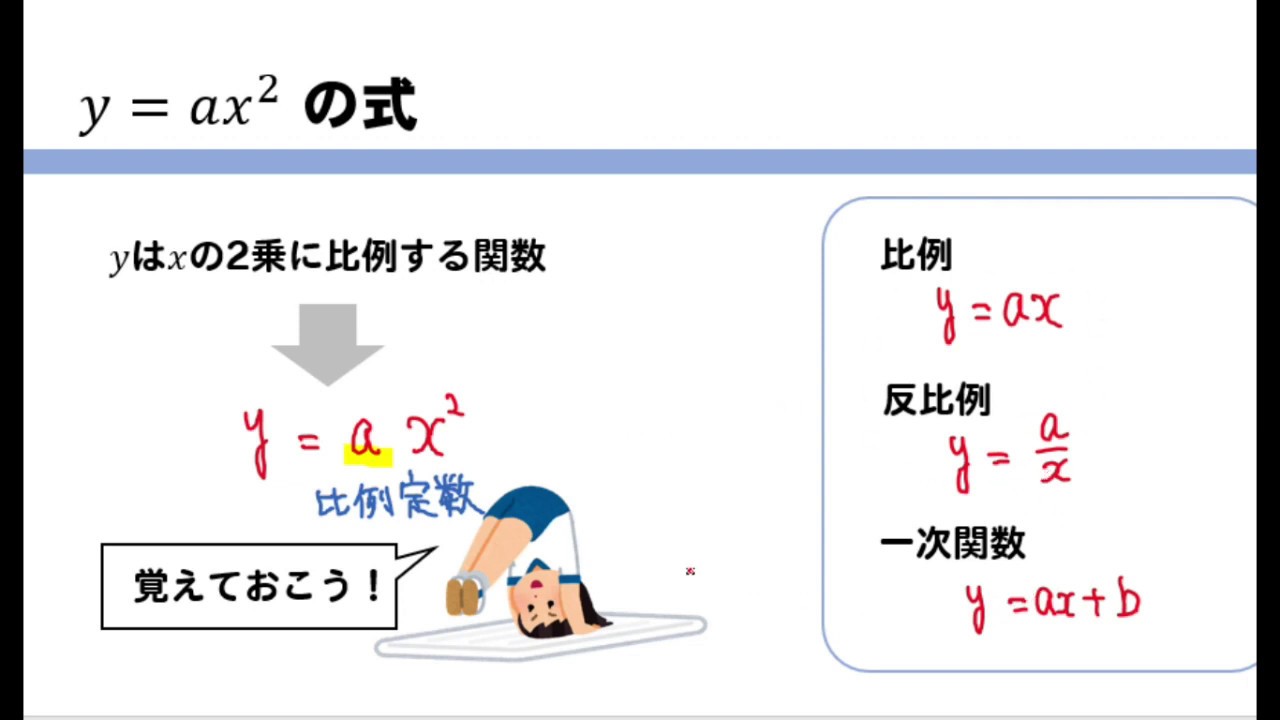
関数y=ax2乗- 2乗に比例する関数の変化の割合は、簡単に求める公式があります。 関数 y=ax2 において、xがpからqに増加したときの変化の割合は、 a(p+q) で求められるのです。 と、実にあっけなく、正解を出すことができます。Y = ax2 y = a x 2 2乗に比例 y y が x x の関数であり、 x x と y y の間に y = ax2 y = a x 2 という関係式が成り立つとき、 y y は x x の 2 2 乗に比例する という。 ただし、 a a は 0 0 でない定数で、比例定数といいます。 「 y y は x x の 2 2 乗に比例する」と問題文に



Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf
式、値の変化、グラフなどから関数関係を分析し、その特徴を理解し、問題を関数的に解決する y = ax2 y = a x 2 の関係にある数量を、表、式で表したり、変数の変域、変化の割合を求めたり、曲線上の2点を通る直線の式を求めることができる 関数 y = ax2 y本時は,関数 y=ax2 の変化の割合について指導する上で,本来ならば変化の割合について学習した 後に扱う平均の速さを先に扱うことで,関数 y=ax2 においても変化の割合を学ぶ必然性を生徒に感じ させ,主体的な学びの姿勢へと導きたい。・関数y=ax2の変化の割 合を求めることができる。 ・関数y=ax2の表,式, グラフを用いて,具体的な 事象を表現することがで きる。 ・関数y=ax2の意味を理 解している。 ・関数y=ax2のグラフや 変化の割合などの特徴を 理解している。
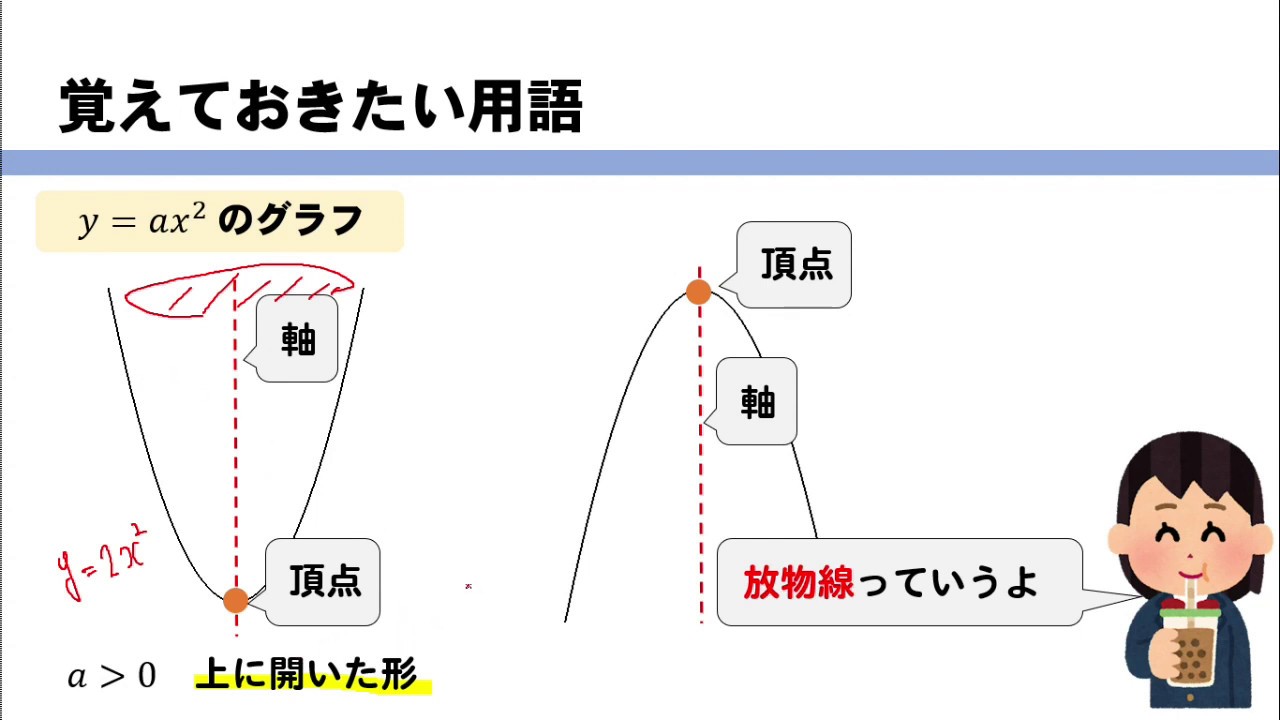
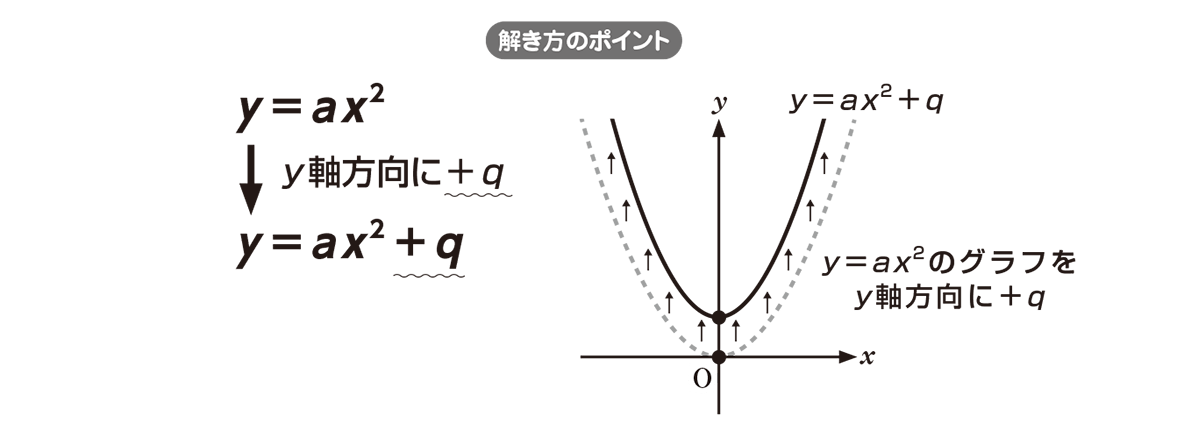
Y 11 2乗に比例する関数 4章 関数y=ax2 重要 yはxの関数で ,y=ax2(aは定数 aŒ0)という式で表されるとき yはxの2乗に比例するという。 関数 y=ax2 で,aを比例定数という。 問題 底面が1辺x cmの正方形で,高さが5 の正四角柱の体積をy 3 とする。 おわりに ここでは、二次関数 y = ax2 q y = a x 2 q のグラフについて見てきました。 このグラフのかき方は、次のようになります。 頂点 (0,q) ( 0, q) を把握し、座標を書く 頂点をもとに、放物線をかく 放物線上のどこか1点の座標を書く 放物線上のどこか21 4章の準備をしよう! 4章 関数y=ax2 17比例の式を求めること変化の割合中学1年中学2年2乗に比例する関数の式を求めていきましょう。 関数y=ax2の式を求めること(本冊p)につながるよ2乗に比例する関数について,変化の割合を求めていきましょう
2乗に比例する関数y=a χ2 の式をつくる。 ・関数y=aχ2 の関係を式で表すことができる。 ・事象の中には、関数y=aχ2 を用いてとらえら れるものがあることを知り、関数y=aχ2の意味 を理解していこれらを受けて、3年生の関数の学習では、「関数y=𝑎𝑥2」について学ぶ。学習を通して、関数 y=ax2 について知るとともに、関数そのものの意味の理解や関数的な見方・考え方を深めさせてい きたい。中3数学。2乗に比例する関数 (y = ax²)。この a は「変化の割合」? xの値が「0から2まで」増加する? 分からん(ガクッ)倒れ込む中学生。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! 2次関数のコツ、成績アップ法を公開。



関数y Ax2乗で Xの変域が 3 X 4のとき yの変域が 4 Yahoo 知恵袋
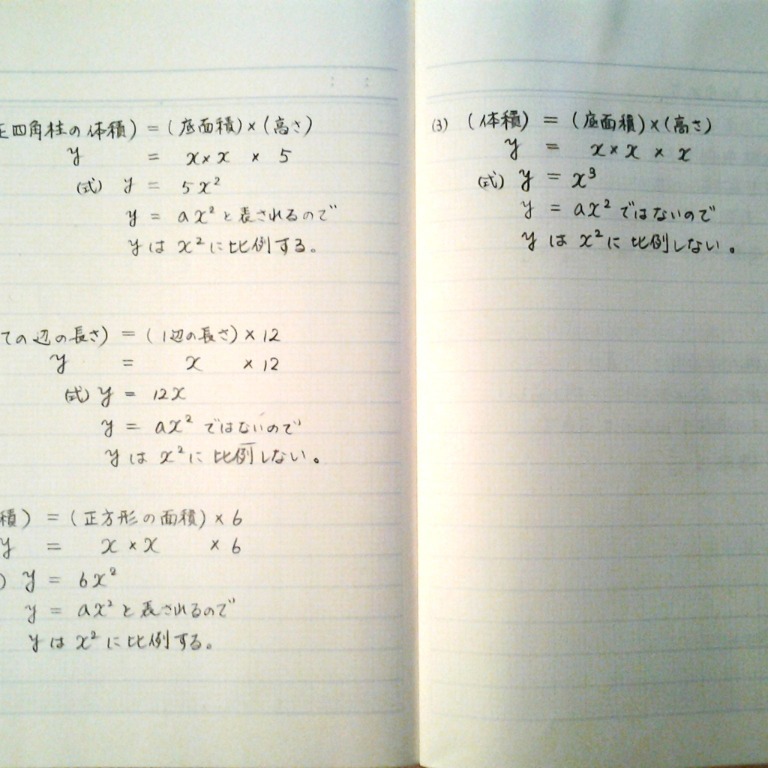



Tossランド 関数y Ax2乗
右図のように2次関数 y=x 2 のグラフと直線 y=x2 のグラフが x 軸, y 軸と交わる点をそれぞれ D , C とするとき,次の問いに答えなさい. (1) 点 C , D の座標を求めなさい. (2) 点 P は2次関数 y=x 2 のグラフ上で x関数y=ax2乗放物線グラフの書き方はこれでバッチリ! yはxの2乗に比例する関数 中3数学y=ax2乗の変域の求め方を解説! 具体例:二次関数y=x^2x5のグラフを作成する手順 中3関数制動距離(y=ax2乗)の利用問題を解説! 中3 関数 y=aX2乗 中学生 数学のノート Clear 表紙 1 2 公開日時 19年12月18日 18時39分 更新日時 21年07月27日 時03分 中学生 3年生 数学



関数y Ax2乗についてxの変域が 2 X 1 Yの変域が0 Y 8である こ Yahoo 知恵袋




y ax2の変化の割合の問題の解き方 現役塾講師のわかりやすい中学数学の解き方
2乗に比例する関数 2乗に比例する関数の式 y=ax 2 (aは比例定数) yの値を求める。 関数はxの値に対応して、yの値が1つ定まるので、関数の式が分かっている場合、 xに値を代入することでyの値を求めることができる。 y=3x 2 で x=2 のときのyの値を求める。 式にxの値を代入するとべ、関数y= ax2 の値の変 化の割合の意 味を見いだす ことができ る。(学習活動 の観察、発表 の様子) 9 関数y=ax2 の式と対応 ・変域 x とy の関係が関数 y=ax2 であるとわか っているとき、その 関係を表す式を求め る方法を知る。 2 関数y=ax2 のグラフきる。関数y=ax2 を、2乗に比例す る関数としてとら 身のまわりにある y=ax2となる関係に 関心をもち、具体的 な事象のなかから関 数y=ax2としてとら えられる2つの数量 を見いだし、式で表 そうとしている。 2 ・関数y=ax2 関数y=ax2の関係



中3 2乗に比例する関数



中3数学 関数y ax二乗 放物線と直線1 発展問題 問題 324 プリント
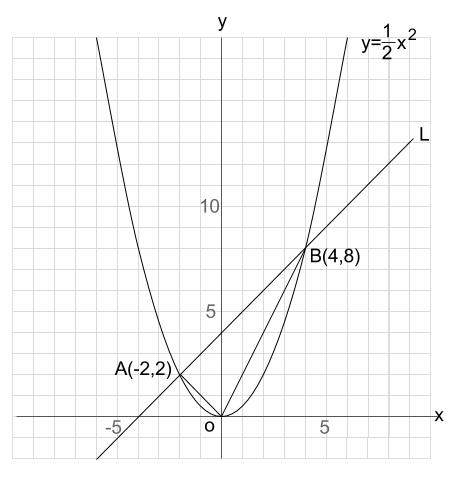
3 関数 y=ax2 KYOKAI 12 13 4 放物線と直線 右の図のように,放物線 y=ax2 と傾き4の直線¬が2点P,Q で交わっている。Pの座標が(1,2)のとき,次の問いに答えなさい。⑴ 直線¬の式を求めなさい。 ⑵ POQ の面積を求めなさい。関数y=ax2乗放物線グラフの書き方はこれでバッチリ! yはxの2乗に比例する関数 関数グラフ上の平行四辺形の座標、面積、二等分線などの問題を解説!関数y=ax 2 と1次関数12x2y5=0でxが4から2まで増加するときの変化の割合が等しくなる。aの値を求めよ。 関数y=ax 2 でxが1から9まで増加するときの変化の割合と、関数y=2x 2 でxが6から4まで増加するときの変化の割合と等しい。aの値を求めよ。




中3 塾ノート 中3数学関数y Ax2乗 中学生 数学のノート Clear




2乗に比例する関数のグラフ 放物線 の書き方 無料で使える中学学習プリント
中3数学。2乗に比例する関数 (y = ax²)。xの値が「p から q まで」増加する時の「変化の割合」、a(pq)?? ダメだ(ガクッ)倒れ込む中学生。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! 2次関数のコツは、これ!(ビシッ) 教科書 新編 新しい数学3 東京書籍, 単元 関数y=ax^2, 「東京書籍中3教科書のp90〜116をまとめました。」, 学年 中学3年生, キーワード 関数このことから、「y はx の2 乗に比例する関数である」とみることができる。 すなわち、2 乗に比例する関数が、 一般的に、a を定数として という式で表されることを理解する。



Mathematics 2乗に比例 2次関数 入試によく出る問題のまとめ 働きアリ The 2nd




関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは Youtube
2乗に比例する関数の性質 解説 関数y=2x 2 について,x=5,4,3,とxの値を代入して計算することにより,次のようなxとyの対応表を作ることができます。4章 関数y = ax2 122乗に比例する関数と図形 学習日 月 日 確認問題1 次の問いに答えなさい。 ⑴ 関数y = ax 2 について,次の①~⑤の場合のa の値をそれぞれ求めなさい。 ① x = 6 のときy = 4 である。 ② グラフが,右の図の放物線になる。 S ③ x の変域が 2 E xE 4数学Gアップシ-ト 3年第4章 関数y=ax2(12) 3年4章 No.12 -ジェットコースターの例で,変化の割合がどんなことを表すか確かめよう- p103 -関数y=ax2と関数y=ax+bの特徴がいえるようにな




関数y Ax2 4 1 6 を教えてください Okwave




中3 Y Ax二乗のグラフの性質 変域の求め方 中学生 数学のノート Clear
1 単元の目標 (1)事象の中には関数y=ax2としてとらえられるものがあることを知ることができる。 (2)関数y=ax2について,表,式,グラフを相互に関連付けて理解することができる。 (3)関数y=ax2を用いて具体的な事象をとらえ説明することができる。Yの変域が0からプラスになっているので,y=ax 2 は上に開いている放物線 (a>0)だということを確認しましょう。 次に,xの変域が2≦x≦4なので, 2≦x≦0の範囲では,関数y=ax 2 は減少する一方で, 0≦x≦4の範囲では,関数y=ax 2 は増加する一方です。2乗に比例する関数とは何か。 永続的理解 2乗に比例する関数は,2つの対応する変数x,yの間の関数関係のうち,xの値がm倍になる と,それに対応するyの値がm2倍となるものである。また,aを定数としてy=ax2という式で



2次関数の各係数の意味




Y Ax2乗 変域の求め方 変域から式を作る方法について解説 中学数学 理科の学習まとめサイト
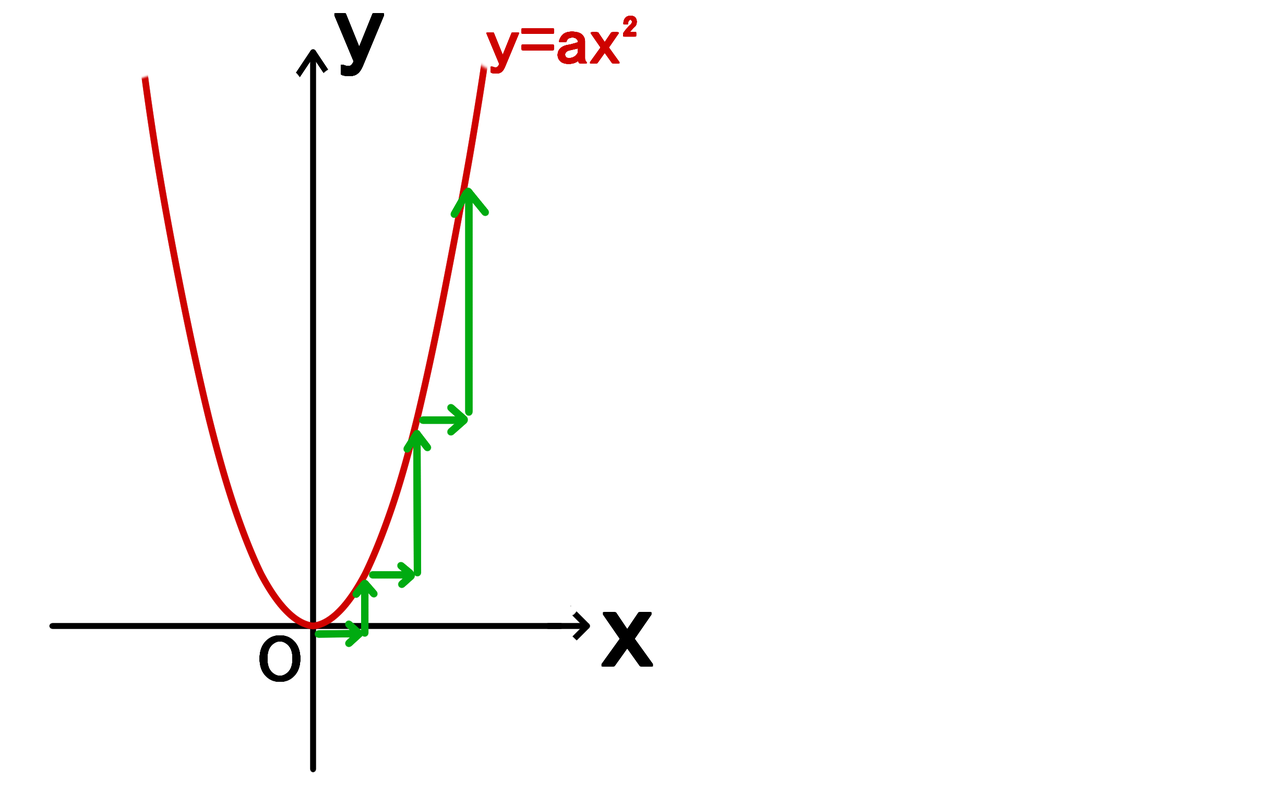
なんで中学教科書では「関数y=ax2」を二次関数と呼ばないの? 中学数学ではなんで「関数y=ax2」を二次関数とよばないの?? こんにちは!この記事をかいているKenだよ。日光にさらされてるね。 中3数学では、夏がすぎたころから、 関数y=ax2 を勉強していく2乗に比例する関数 解説 一般的に,「 は〇に比例する」という関係は, =(定数)×〇 という形で表されます。そのため,2つの変数x,yの間に, y=ax 2 (a≠0) の関係があれば,yはxの2乗に比例するといい,aを比例定数といいます。4 関数y=ax2 のグラフと変域(1) VMA05 3 2 乗に比例する関数の増加・減少 ここでは,関数y=ax2 の値の増加・減少について学習してみましょう。 関数y=ax2 でxの変域が与えられたときのyの最大値・最小値は,たとえばa>0 のとき のように, xの変域によって考え方が違ってきま




例題で学ぶ高校数学 Y Ax2 Q




関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ




中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく



Q Tbn And9gcqaprtvg0neilnjo9asyuyrm98yhmbqq 0ommpdn1uewjgqu E7 Usqp Cau



Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf




2次関数の基本的問題だが実は重要な問題 中学数学 理科 寺子屋塾の復習サイト




数学3年 2次関数 Y Ax2 2次関数のグラフ 2次関数の変域 2次関数の応用 2次関数のグラフ Xの2乗に比例する関数 問題1 正解1 解説1 問題2 正解2 解説2 問題3 正解3 解説3 問題4 正解4 解説




Y Ax 2 Bx Cのグラフ 数学i フリー教材開発コミュニティ Ftext




中3数学講座第4章関数y Ax2乗 2 Y Ax2乗のグラフ基本問題 Youtube




Y Ax2乗の利用 放物線と直線による面積 中学3年の問題をイチから解説 中学数学 理科の学習まとめサイト




中3数学 Y Ax 2のグラフ A 0 映像授業のtry It トライイット



Www Shinko Keirin Co Jp Keirinkan Tea Chu Kakudai Pdf Chusu B5 3nenh Pdf




中3数学 Y Ax2乗の変域の求め方を解説 数スタ




関数y Ax 2 の勉強法のわからないを5分で解決 映像授業のtry It トライイット




関数y Ax 2 の勉強法のわからないを5分で解決 映像授業のtry It トライイット



関数y Ax の 変化の割合 の問題 Xの値がaからa 2まで増加したときに Yの値は バカでもわかる 中学数学



明日テストなので 早めの回答願います 中3数字関数y Ax2乗に Yahoo 知恵袋



関数y Ax2乗グラフ利用の問題が分からないため 解説付きで教えて下さ Yahoo 知恵袋




中3数学 Y Ax 2の増減 映像授業のtry It トライイット
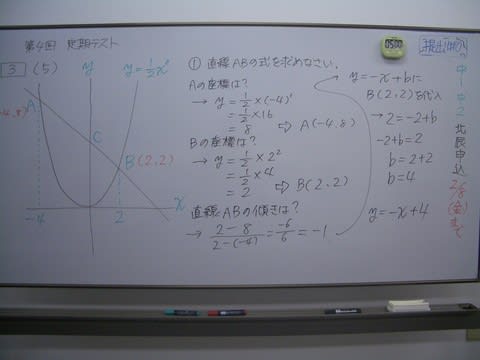



中3数学 篠津中 第4回定期テスト対策 関数y Ax2乗 面積の2等分線 ブログ アビット




二次関数y Ax2の比例定数の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




関数y Ax 2 の勉強法のわからないを5分で解決 映像授業のtry It トライイット




関数y Ax2乗 変域の求め方 変域から式を求める問題を解説 Youtube



Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf




中学3年 関数 Y Ax2乗 利用 Clear




なんで中学教科書では 関数y Ax2 を二次関数と呼ばないの Qikeru 学びを楽しくわかりやすく




関数y Ax2乗のグラフの書き方を教えてください ཀ Clear



3 X Y Lihat Cara Penyelesaian Di Qanda



数学の問題です 図のように関数y Ax2 2乗 のグラフ上に3点a B Yahoo 知恵袋
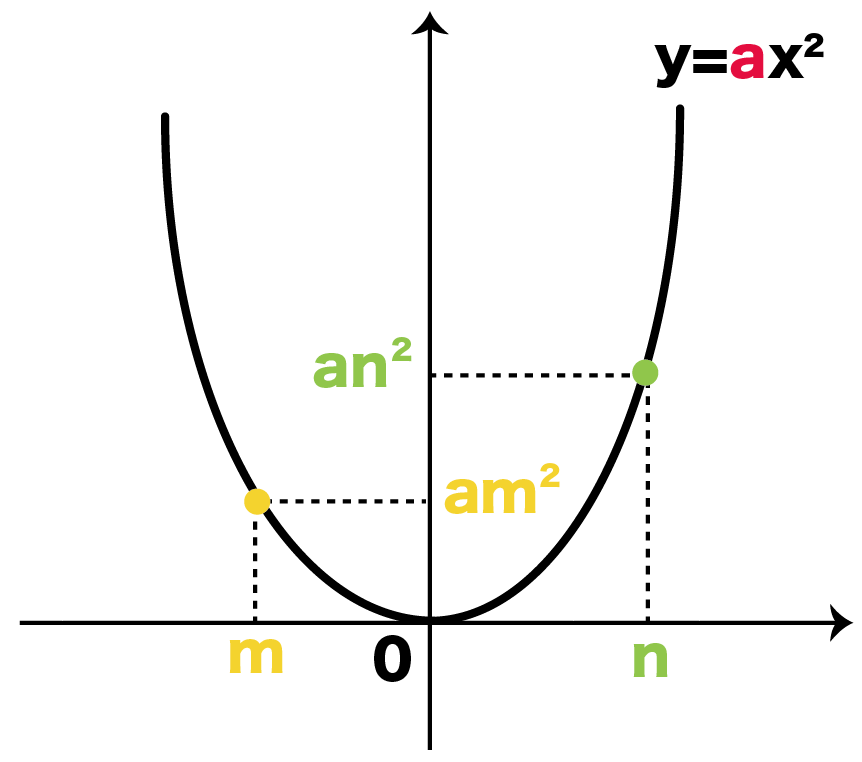



二次関数y Ax2の変化の割合を3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
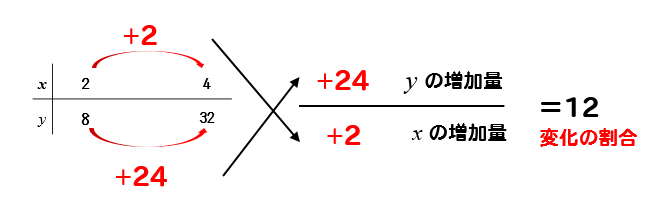



変化の割合 二次関数y Ax2の裏ワザ公式 どうやって解くの 数スタ




スタディピア 関数とグラフ




中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ 関数 グラフ 学習



直線lが 関数y Ax2乗のグラフおよびx軸と右の図のように3点a b cで交 Yahoo 知恵袋




高校数学 2次関数のグラフy Ax Bx Cの係数の符号 受験の月
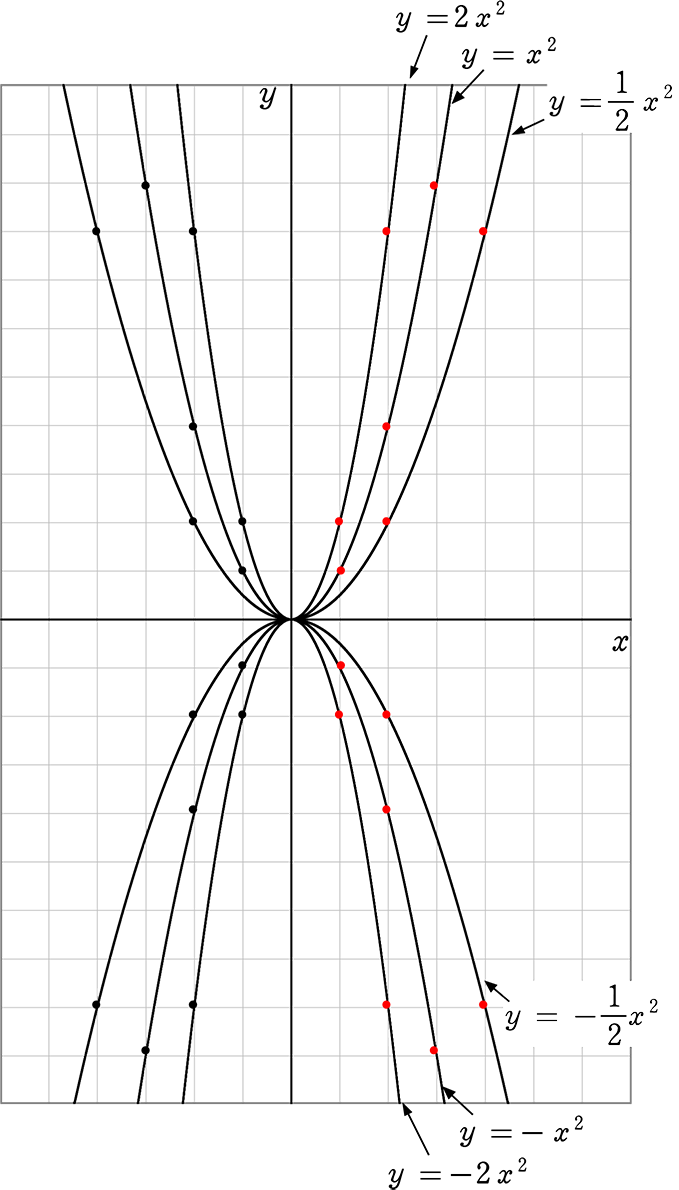



中学数学 関数



関数yax2乗 表 ニスヌーピー 壁紙




高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット



Www Shiga Ec Ed Jp Www Contents Files Kannsuu Pdf



関数y Ax2乗の変域の求め方 勉強ナビゲーター




一次関数とy Ax2乗の変域の解き方を分かりやすく教えてください 例題なんで Clear



数学問題の出題範囲詳細




違うアプリで聞いた時に y Ax2条の時はグラフは上にひらくって聞いた 数学 教えて Goo



Http Www Ikushin Co Jp Shuppan Textimg 16jack Chu3hyo Sugaku Hon Pdf



文字係数2次関数の頂点
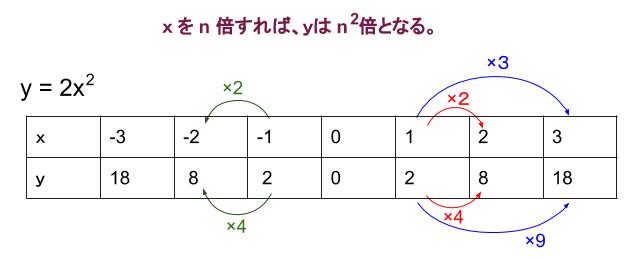



中学数学 Y Ax 2 2乗に比例 導入 中学数学の無料オンライン学習サイトchu Su



9hfjyz6uor2xnm



右の曲線は 関数y Ax2乗のグラフである これについて 次の Yahoo 知恵袋




関数y Ax2乗 変化の割合の裏ワザ公式 どうやって解くの Youtube



関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは Youtube



1




基本 二次関数 Y Ax 2 のグラフ なかけんの数学ノート



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ Youtube
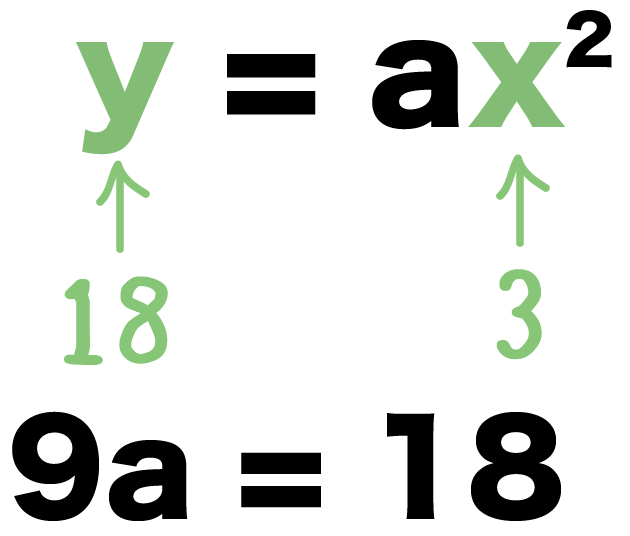



二次関数y Ax2の比例定数の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



高校数学 Y Ax 2 Qのグラフ2 映像授業のtry It トライイット




2番の解き方を教えてください お願いします Clear




スタディピア 関数とグラフ




中学数学 Y Ax 2 図形との融合問題 中学数学の無料オンライン学習サイトchu Su




中3 塾ノート 中3数学関数y Ax2乗 中学生 数学のノート Clear




二次関数y ax 2 のグラフは点a 4 2 を通っている y線 数学 教えて Goo




なんで中学教科書では 関数y Ax2 を二次関数と呼ばないの Qikeru 学びを楽しくわかりやすく



2次関数の公式について質問があります Y Ax2乗 Bx Cと Yahoo 知恵袋




人気ダウンロード 関数yax2乗 グラフの利用 ニスヌーピー 壁紙



年前期 千葉県公立高校入試前期 数学 第2問 1 Y Ax2の変域 問題 解答 解説 動画解説 文字解説両方あり 船橋市議会議員 朝倉幹晴公式サイト




関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ




Kelas 9 Catatan Tentang 数学 y Xの二乗の値の変化 Clear




Mathematics 2次関数 2乗に比例 の 変化の割合 を簡単に求める方法 働きアリ




中3関数 制動距離 Y Ax2乗 の利用問題を解説 数スタ



Y Ax 2



Www Pref Hiroshima Lg Jp Uploaded Attachment Pdf



Q Tbn And9gcr6dtilpwb5qobpe1maa3yl 4gtdluqqzealqycb Gjav3drt S Usqp Cau



大問1の 1 で関数y Ax2乗の式の変化の割合は一定ではないのにな Yahoo 知恵袋



Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf




二次関数y Ax2の変化の割合を3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




中学3年生 数学 2次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



は それぞれ関数y Ax2乗 y 4 y 1のグラフである Yahoo 知恵袋



野並英館塾ホームページ 中学数3 関数 Y Ax2




例題で学ぶ高校数学 Y Ax2




Y Ax2乗 Aの求め方についてパターン別に解説 発展問題もアリ 中学数学 理科の学習まとめサイト



Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf




中3数学 関数y Ax2乗 3 Y Ax2乗値の変化と変域 Youtube




二次関数y Ax2の比例定数の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Y Ax 2




中3 関数 Y Ax2 まとめ 中学生 数学のノート Clear



Q Tbn And9gcts4ooisg5hhpkj19vm7nks1wpas2lwfm530j7bmkcaxug8oixu Usqp Cau



Www Kyo Kai Co Jp Img Material Chuu 3517s A S3 Mihon Pdf



2




2次関数のグラフ




2次関数のグラフと直線



0 件のコメント:
コメントを投稿