[ベスト] ベクトル 長さ 計算 234171-ベクトル 長さ 計算機

そして、ベクトルの和の長さ(速さや大きさ)は、三平方の定理を使って、次の式で表すことができます。 \(\vec{a}\vec{b} = \sqrt{(x_1x_2)^2(y_1y_2)^2} \) これらの式を頭に入れておくと良いでしょう。を描くとき、点の位置ベクトル⃗rは、⃗r = ⃗r(t)と表される。この式を曲線 のベクトル方程式といい、tを媒介変数（パラメター）とよぶ。このよう に、一般にベクトルA⃗ の各成分がそれぞれ実数tの関数であるとき、つ まり、A⃗ = (a単位ベクトルの求め方 の分母はスカラー，分子はベクトルであることに注意して下さい。 \overrightarrow {a} a と同じ向き。 = 1 より大きさが1，つまり単位ベクトル。 今持っているベクトルをその長さで割れば同じ方向の単位ベクトルが得られるという訳

空間ベクトルの垂線の足や長さの求め方 Den Of Hardworking

ベクトル 長さ 計算機

ベクトル 長さ 計算機-ベクトル計算には 1 次元の計算とは明確な類似点のないメソッドがさらに 2 つあります。外積と内積です。外積は、2 つの既存のベクトルに対して(90 度で)直交するベクトルを生成する手段です。たとえば、x 軸と y 軸の外積は z 軸です。N ) {// Z軸に平行な平行線分を書く。 float ratio = n / (10f * numOfMesh);float offset = ratio * width;DrawLine3D( VGet(x0 offset, 00f, z0), VGet(x0 offset, 00f, z0), lineColor );}for(int n = 0;

物理のための数学 ベクトルの外積 お茶処やまと屋

ベクトルの複素数表現と、複素数による合成計算例 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会 交流回路は、ベクトルを用いて計算することができる。 ベクトルは図形を基本としたものであるが、図形に頼るだけでは複雑な回路にベクトルの大きさ ベクトル a → = ( a 1 , a 2 ) {\displaystyle {\vec {a}}= (a_ {1},a_ {2})} に対してこのベクトルの大きさは、 a → = a 1 2 a 2 2 {\displaystyle {\vec {a}}= {\sqrt { {a_ {1}}^ {2} {a_ {2}}^ {2}}}} で与えられる。 導出 上のベクトル a → {\displaystyle {\vec {a}}}Y = diff (X) は、サイズが 1 でない最初の配列の次元に沿って、 X の隣接する要素間の差分を計算します。 X が、長さ m のベクトルの場合、 Y = diff (X) は長さが m1 のベクトルを返します。 Y の要素は、 X の隣接する要素間の差分です。 Y = X (2)X (1) X (3)X (2

Y=f (x) y = f (x) なる関数で表される曲線があるとします。 そして a, b a,b での弧の長さを計算してみましょう。 n n 分割して考えます。 AB AB に近似できます。 L L は次のように計算できます。 Δs = ds は 線素 といいます。 ベクトル解析などで注釈なしで面の法線ベクトル は、幻日環の場合と同様に、 と表わされる。 これを用いて（8）式のベクトル表記した屈折の法則 より、氷の結晶の側面から出て行く屈折光ベクトル を計算すればよいのであるが、簡単な計算で、 = − 1 sin ・・・（14）B = c v e c t o r お客様の声

N ) {// X軸に平行な平行線分を書く。= √ 6400 = √ 800 = よっ√0 * 0 0 * 0 =>

外積とは何か ベクトルの外積の定義 意味 大きさについて アタリマエ

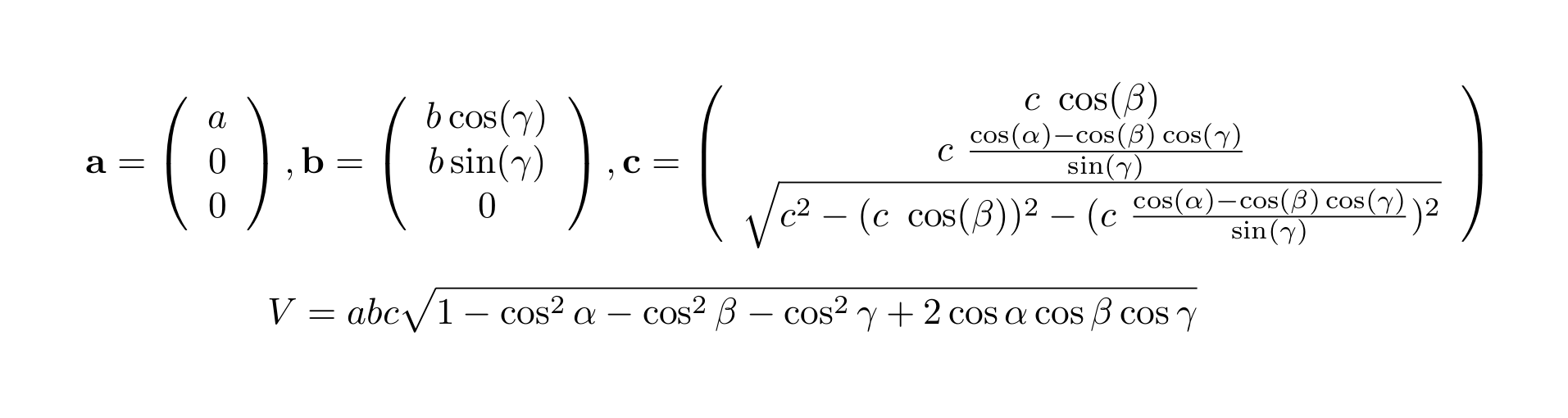
逆格子点の計算の理論背景 Theoretical Background For Calculation Of Reciprocal Lattice And Reciprocal Lattice Points To Cause Diffraction

ベクトル空間モデルにおいて、文書間の類似度を調べる手法です。 cos類似度を計算することによって、文章の似てる度合いを計算できます。 c o s ( A, B) = A B A B 分母はそれぞれの文書ベクトル長をかけ合わせたもので、 分子は文書Aと文書Bの内積(x, y) = (10, 40) 2点間のベクトル x成分 = 10 10 y成分 = 40 40 ベクトル =>例 2次元ベクトル (1,80)の大きさ (長さ)を求める = √ 1²

３点の座標から簡単に角度と回転方向を求める 2 3 N次元 外積を用いる方法

高校数学b 内積の計算公式とその応用 映像授業のtry It トライイット

2次元ベクトル (x,y)の場合は、ピタゴラスの定理で簡単に大きさを求めることができます。 2次元ベクトル (x,y)の大きさ = √ x²For(int n = 0;ベクトル同士の計算 同じ長さ同士のベクトルの演算 (算術演算，論理演算，比較演算) は，対応する各要素の演算となる．すなわち，普通の数字と同様に (加算)， (減算)， * (積)， / (商)， %/% (整数商)，%% (剰余)，^ (べき乗) が行える．

ユークリッド空間r Nの内積 ノルム 距離について解説 趣味の大学数学

Processing ベクトルを扱ってみよう 世界はフラクタル

一つは行列の列数nとベクトルの長さnが等しい場合のみ積が求められるということ、もう一つは結果が長さmのベクトルになるということです。 なお、 A ⋅ x の各行は行列 A の各行とベクトル x の内積になっているということも分かります。ベクトルのノルム（大きさ、長さ） ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = a n a a M r 1 ベクトル に対して a a rr a r をのノルムといい a と表す。 r 2 2 1 L= a a a n r 空間内の幾何ベクトルの作る線形空間に対しては、 ノルムとベクトルの大きさは同じ意味である 正規ベクトルv,tの長さを求めるのに平方根を2回も使うのは処理速度的にどうかと思いますので、両辺を二乗してsqrtを外したり、あらかじめミサイルの速度がわかっていればsqrt(vx 2 vy 2)の代わりにするなど、工夫してください。

ベクトルの大きさ

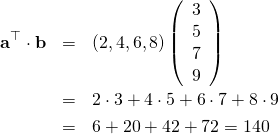
内積 ベクトルの内積 とは 定義 公式 計算例 意味 英語訳 線形代数 K San Link

Struct vector2 { T x, y;Y) x(x), y(y) {} // ベクトルの長さ T(x, y) = (10, 40) 終点 =>

平行四辺形の面積 ベクトルでの公式 理数系無料オンライン学習 Kori

ベクトルの大きさの最小値 ベクトルの大きさの最小値とその時のtの値 数学 教えて Goo

ベクトルの内積abは、aとbが同じ次元の場合のみ乗算が可能です。 ベクトルの外積a×bは、aとbが3次元の場合のみ乗算が可能です。 inner product a⋅b =c scalar cross product a×b =c vector i n n e r p r o d u c t a ⋅ b = c s c a l a r c r o s s p r o d u c t a ×This structure is used throughout Unity to pass 3D positions and directions around It also contains functions for doing common vector operations Besides the functions listed below, other classes can be used to manipulate vectors and points as well For example the Quaternion and the Matrix4x4 classes are useful for rotating or transformingベクトルの長さの計算式 物体間のベクトルが計算できれば物体間の距離も分かります。 数学的にはこんな計算式です。 長さ = √( (x*x)(y*y)(z*z) ) D3DXVec3Length DirectXのD3DXVec3Lengthでベクトルの長さが分かります。 FLOAT out = D3DXVec3Length( D3DXVECTOR3 *in )

3 外積の大きさ

ベクトル １６ 空間ベクトルの内積計算 怜悧玲瓏 高校数学を天空から俯瞰する

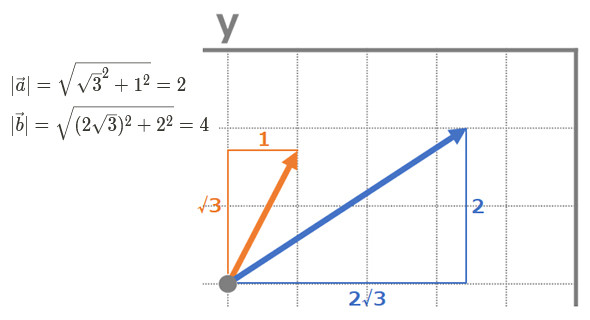
(メモ) ベクトルの長さを知るには、関数を使用して「length(変数)」とします ベクトルに対しても四則演算・巾が適用できます 引き続いて以下のように試してください ベクトルの対応する要素毎の四則演算・巾を計算していることに気づくでしょう32 ベクトルの内積と長さ(ノルム) ベクトルの内積と長さの計算も容易にできる。ここではa = 1 2 3T とb = −3 −2 −1T を例に，MATLAB で内 積と長さの計算方法について確認する。 まず，ベクトルa とb を代入する。必ず縦ベクトルとして入力すること。 >>ベクトルの計算方法を解説するために、例として次のような2つのベクトルを考えます。 今回は2次元（要素が2つ）のベクトルで、次のような数字の集まりとします。 ベクトルa（オレンジ色）、ベクトルb（青色）の図 Pythonのリストで表現すると、次の

外積を利用した2つのベクトルに垂直なベクトルの求め方とは 大学入試数学の考え方と解法

ベクトル３

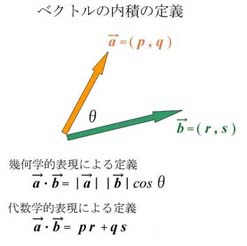
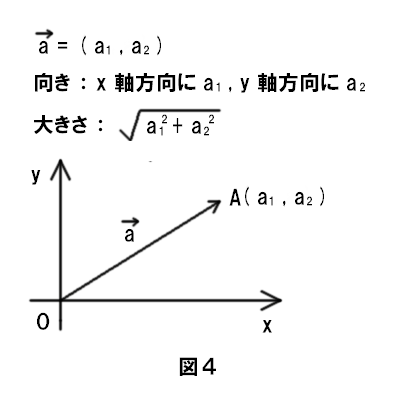
ベクトルの長さ ベクトル \(\vec{\ a\ }=(a_1,a_2)\) に対して このベクトルの長さは \(\vec{\ a\ }=\sqrt{{a_1}^2{a_2}^2}\) で表されます。ベクトルの長さを求めるのは、時と場合により、そう簡単じゃないことがあります。 そこで、以下にベクトルの長さを求める公式を書きます！ ！ ！ a → ⋅ a → = a → 2 どうですか？ この公式によると、自分自身とのベクトルの内積が、自身のベクトルは，数値あるいは記号値の簡単なリストからなる n 次元ベクトル空間内のオブジェクトです． WolframAlphaは，ベクトルを球座標系あるいは極座標系に変換し，ベクトル長や正規化等のベクトルの特性を計算することができます．

空間ベクトルの垂線の足や長さの求め方 Den Of Hardworking

無料ダウンロード X ベクトル 書き方 100 イラスト

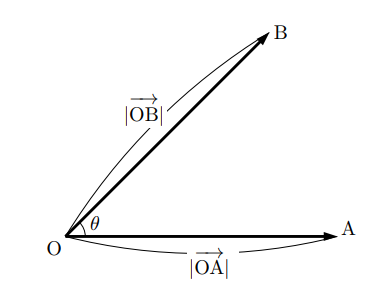
面の法線ベクトル= (Sl, Sm, Sn) (θの範囲を考慮し、符合を反転させます) 光線の方向ベクトル= (L, M, N) 方向余弦 とします。ともに絶対値は1です。両ベクトルのなす角をθとし、内積を計算すると Sl * L Sm * Sn * N = cosθ (正負の符号を考慮)大きさが5のベクトルを5で割ると大きさ1のベクトルになります(向きは変わりません)。 一般に，ベクトル をその大きさ で割ったもの は， と同じ向きで大きさ1のベクトルになります。内積 (ベクトルの内積)とは？ 定義・公式・計算例・意味・英語訳線形代数 ベクトルの内積には2種類の定義の仕方があります．ひとつは長さと交角による定義で，もうひとつはベクトルの成分の積和による定義です．内積は2次元平面上のベクトルに

3

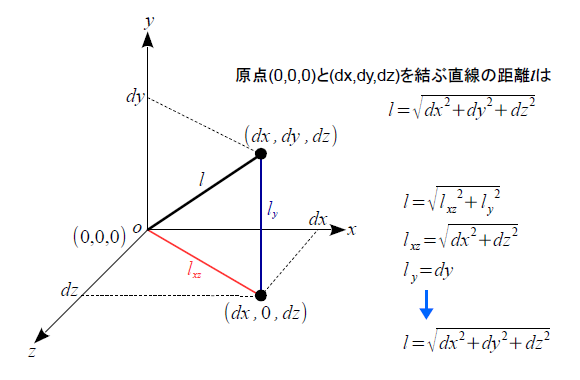
数学関数 ２点間の距離 ３次元 ゆるゆるプログラミング

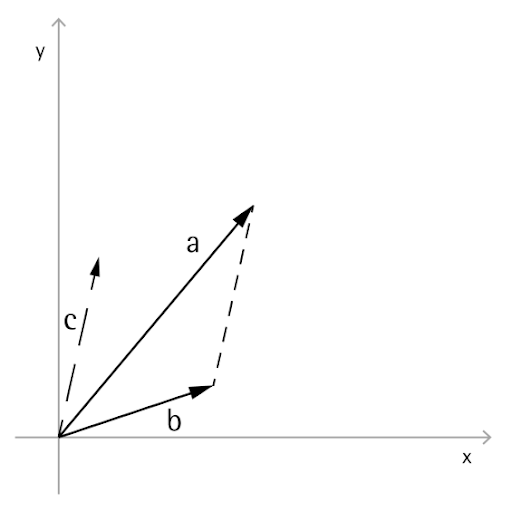
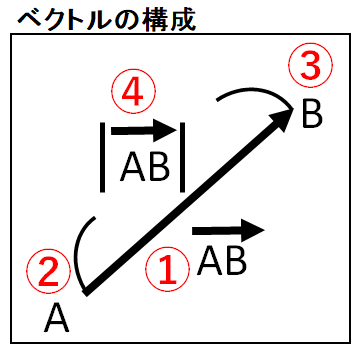
// sqrt template <class T>これらのベクトルは = 2 i 2 j 、 = 0 i 3 j = 3 j と表すことができます。 例題は2次元ベクトルを使っていますが、以下に述べる方法は成分の数がいくつであっても適用できます。ベクトルは 平行で長さが等しい ものは始点がどこであれ 同じベクトル である と定義されています。 なので和を考えるときに、 始点が揃っていなければ揃えてから 始めます。 例えば このような 2 つのベクトルの和を考えたい場合は

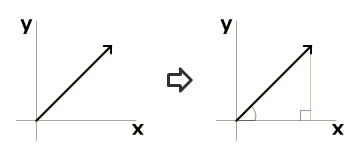
ベクトルの大きさ 長さ を求める計算式と計算ツール Peko Step

ベクトル内積の意味をイメージで学ぶ 射影とは なす角とは ばたぱら

(x, y) = (0, 0) 長さ =>零ベクトルは、単位ベクトルと違って「向きなし、長さ0」という唯一のベクトルを表すため、これを「\(\boldsymbol{o}\)」という記号で表します。 これらみんな高校で習ったよね？笑 ベクトルの計算 ベクトルの足し算ベクトルの長さは，それぞれの成分の2乗の和の平方根になります． つまり，ベクトル \mathbf{v} = (v_x,v_y,v_z) があったとすると， 次のような式になります．

空間ベクトルとは 内積 面積などの公式や問題を解くコツ 受験辞典

Excel Vba 数学実験室 ベクトルの大きさを計算しましょう

A * b1 2 6 12以下は、計算のイメージです。a1 * b1 ⇒ 1 2 ⇒ 2a2 * b2 ⇒ 2 3 ⇒ 6a3 * b3 ⇒ 32つのベクトルが作る回転行列を計算 (スクリプト) Pythonスクリプトで、2つのベクトルが作る回転行列を計算します。 numpyを使用しています。実数の意味と例（0、負の数、）および実数でないものの例 式の展開（やり方、公式、ツール） (abc)^2、 (abc)^3の展開公式 因数分解を自動で計算してくれるツール 3乗の因数分解公式5つと例題 a^2 (bc)b^2 (ca)c^2 (ab)の因数分解など 複二次式の因数分解のやり方と例題5問 a^3b^3c^33abcの因数分解と応用問題2問 因数分解公式一覧（全22個）

ベクトル計算 Dynamo Primer

ゲーム数学 ベクトルの基礎

最初のページ はじめに 1 座標系と長さの概念 11 初等幾何学での作図 12 座標系の約束 13 長さの理解 14 コンピュータベクトルを定数倍すると，方向が変わらずに大きさだけ何倍かされます．（正の数を掛ければ同じ向きに何倍かされ，負の数を掛けると逆向きに何倍かされます．）そこで，与えられたベクトル と同じ向きの単位ベクトルを作るには，その大きさ で割ればよいことになります．

平面幾何におけるベクトル演算 内積と外積

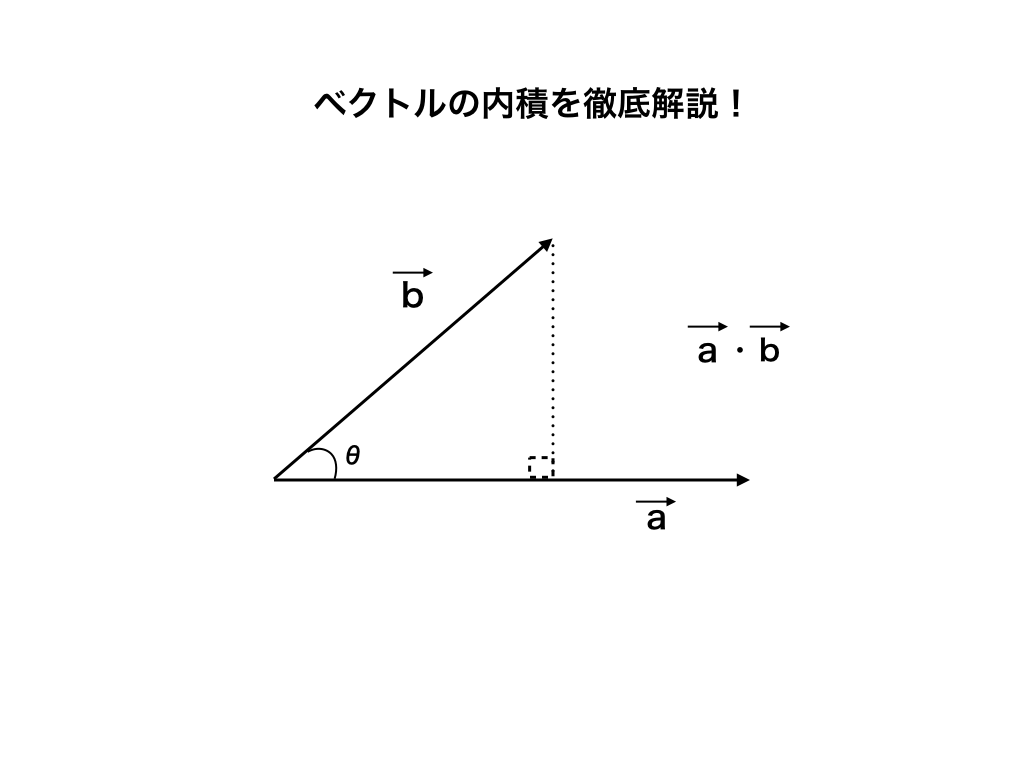
内積とは 定義と求め方 公式を解説 ベクトルの掛け算を分かりやすく

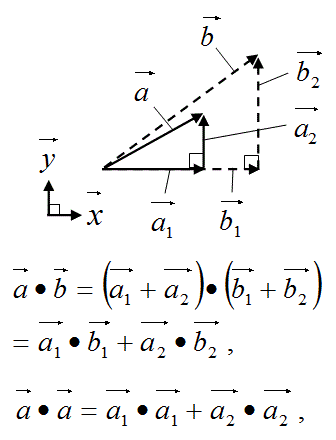
勉強しよう数学 ベクトルの内積の和と積の公式

ベクトルの内積

高校数学b 余弦定理のベクトル表示と内積の定義の成分表示の証明 受験の月

ベクトル

1

ベクトルの内積 スカラー積 と外積 ベクトル積 の成分表示

物理のための数学 ベクトルの外積 お茶処やまと屋

高校物理 便利なベクトルで 変位 速度 加速度 力学 お茶処やまと屋

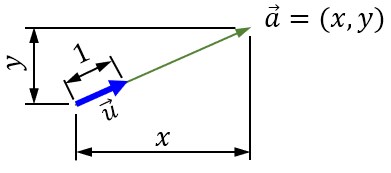
単位ベクトルとその応用 イメージングソリューション

内積とベクトルの長さ

Excel エクセルで単位ベクトルを計算する方法 単位ベクトルの求め方

平面ベクトルの定義と公式 足し算 絶対値 内積 なす角の求め方 Irohabook

ベクトル １６ 空間ベクトルの内積計算 怜悧玲瓏 高校数学を天空から俯瞰する

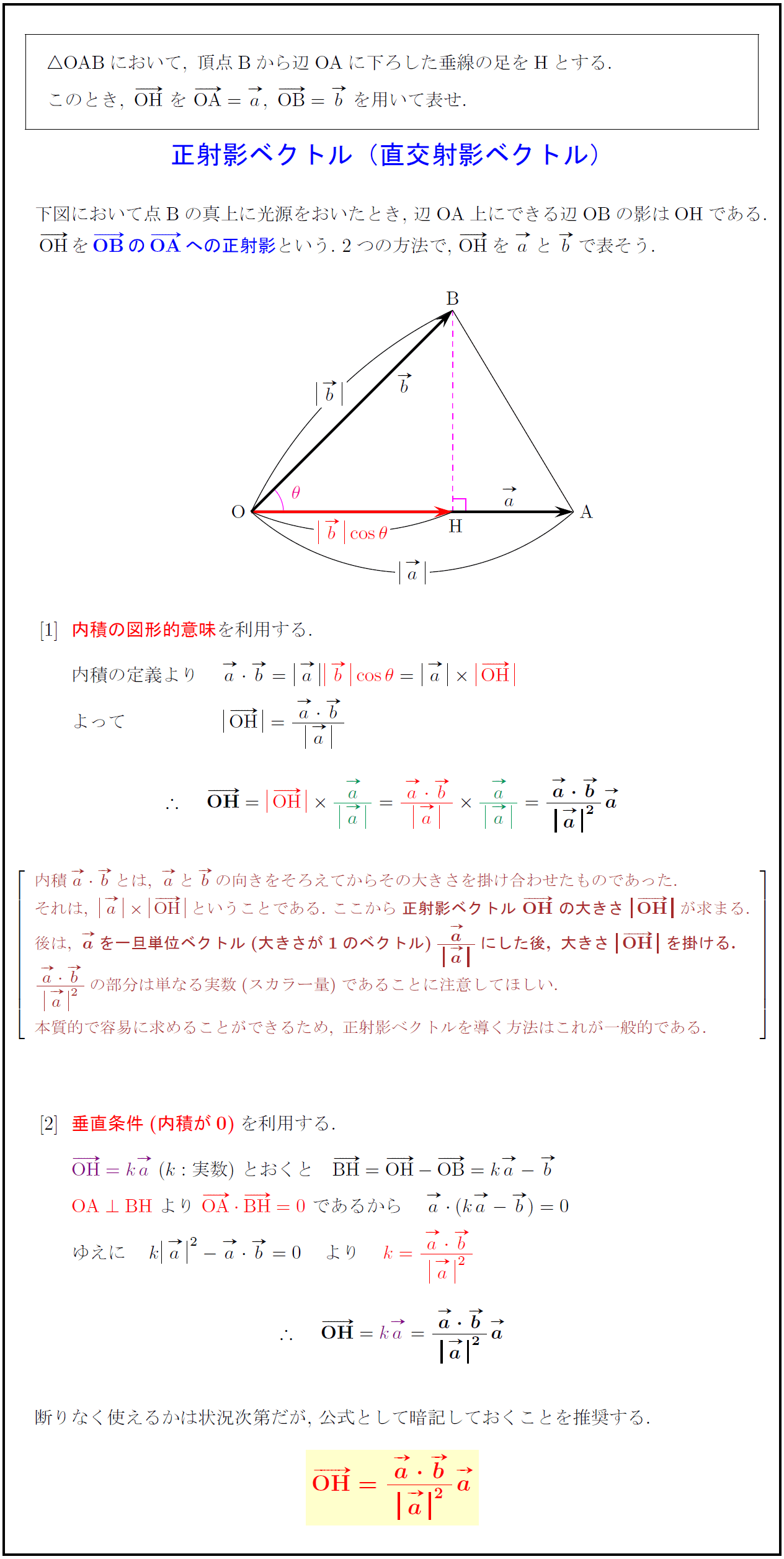
高校数学b 正射影ベクトル 直交射影ベクトル 受験の月

ベクトルの内積 スカラー積 と外積 ベクトル積 の成分表示

ベクトルの和と差 大きさの計算 電験3種ネット

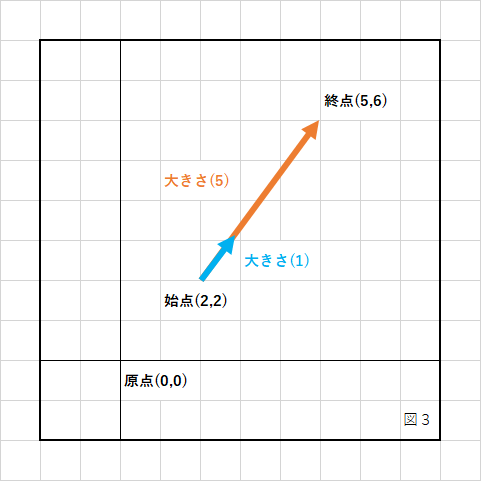
ベクトルについて

青チャート 空間ベクトルの内積 Clear

成分表示された空間ベクトルの大きさ 数学b フリー教材開発コミュニティ Ftext

高校数学b ベクトル A Tb の大きさの最小値と図形的意味 受験の月

数学b 単位ベクトルの求め方とは 平行 垂直な場合の求め方も解説 数スタ

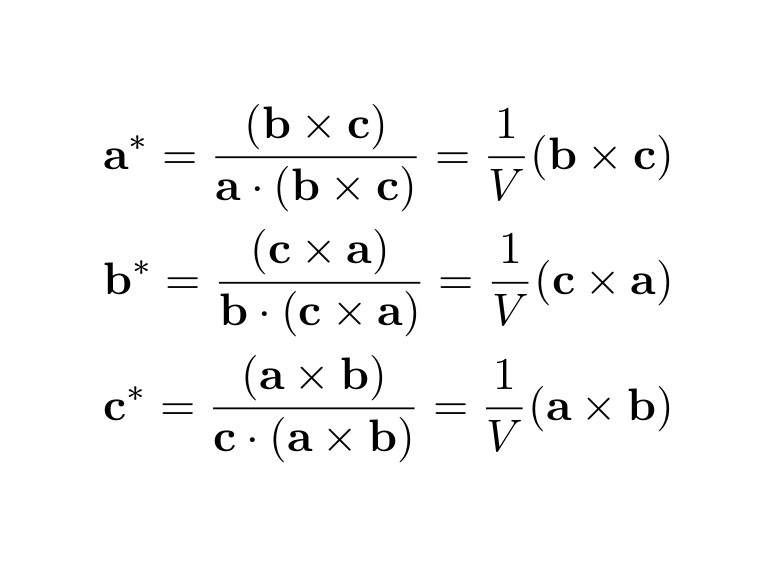
逆格子点の計算の理論背景 Theoretical Background For Calculation Of Reciprocal Lattice And Reciprocal Lattice Points To Cause Diffraction

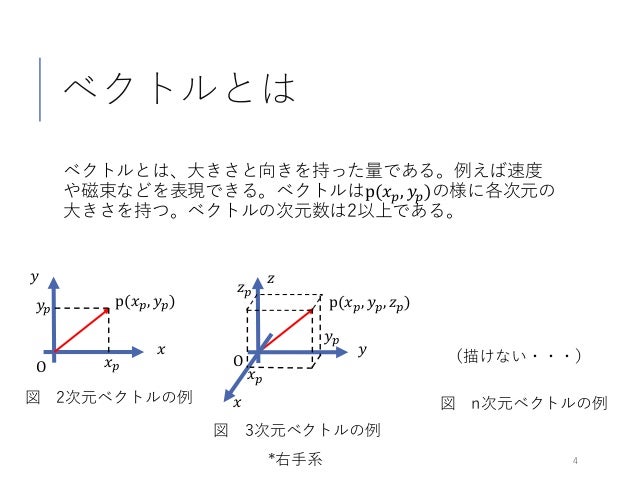
Vbaで数値計算 07 ベクトル

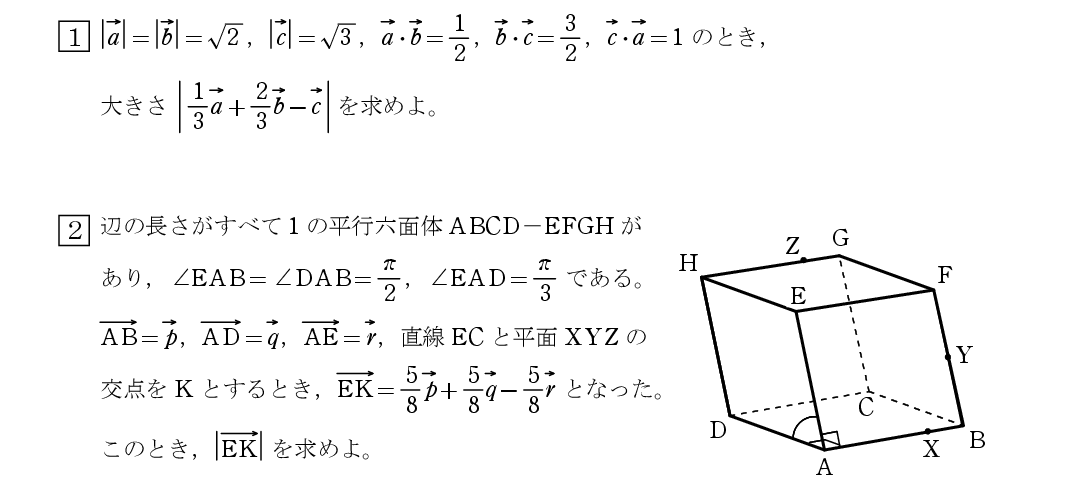
ベクトル １５ 空間ベクトルの大きさ計算 怜悧玲瓏 高校数学を天空から俯瞰する

ゲーム数学 ベクトルの基礎

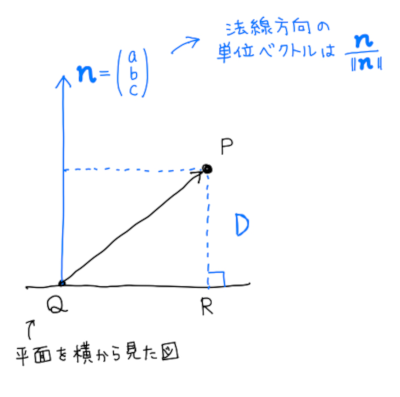
点と平面の距離 ベクトル解析 基礎からの数学入門

高校数学b ベクトルの内積 ２ 映像授業のtry It トライイット

ベクトルの内積 スカラー積 と外積 ベクトル積 の成分表示

ベクトル大きさ求め方について質問です Op A B O Yahoo 知恵袋

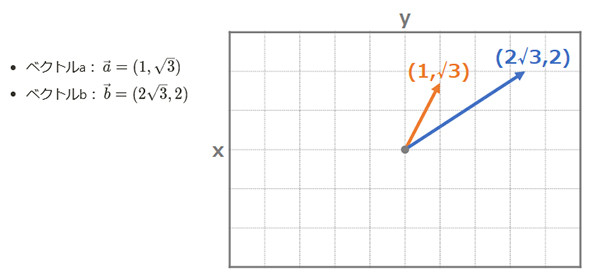
統計学や機械学習でもよく使われる相関係数が分かるベクトル計算の基礎知識 Ai エンジニアになるための 基礎数学 再入門 12 It

ベクトルの和と差 大きさの計算 電験3種ネット

ベクトルの公式一覧 計算 内積 三角形の面積 共線条件 理系ラボ

Q Tbn And9gctcio2bnqgqd09 Pmwlvkh Qdt8pbepmprsvzkzg Fqyznuyvfz Usqp Cau

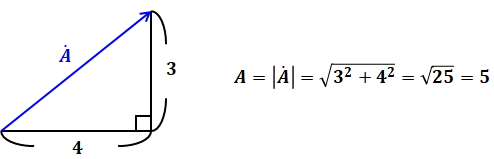
ベクトルの大きさ 電験三種 これでok

ベクトルの大きさとは 1分でわかる意味と求め方 記号 二乗 絶対値との関係

内積とは ベクトルの内積の意味 公式 求め方などをスッキリ解説 遊ぶ数学

ベクトルの平行条件 垂直条件とは 内積公式や証明 計算問題 受験辞典

ベクトル編 高校のベクトルを基礎から復習 A 大学1年生もバッチリ分かる線形代数入門

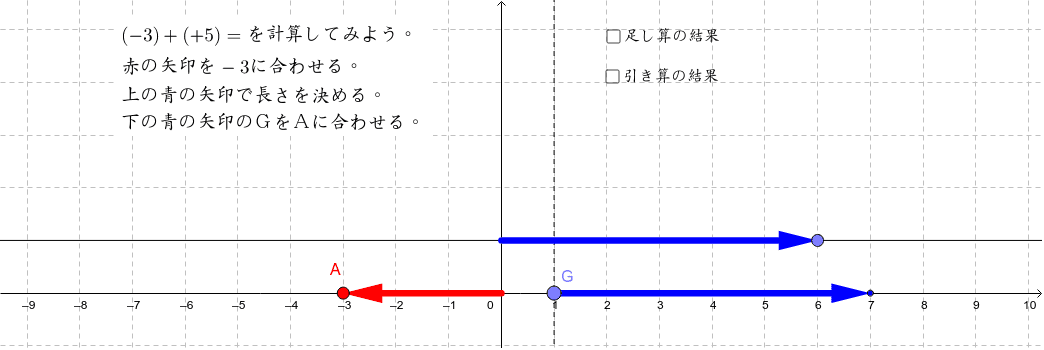
正の数と負の数の計算 ベクトル Geogebra

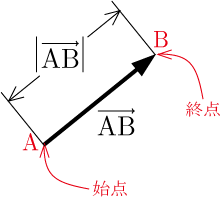
ベクトルの大きさ

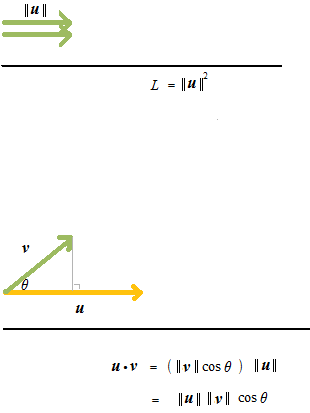
621 ベクトル 内積 外積 Tokyomaths Com

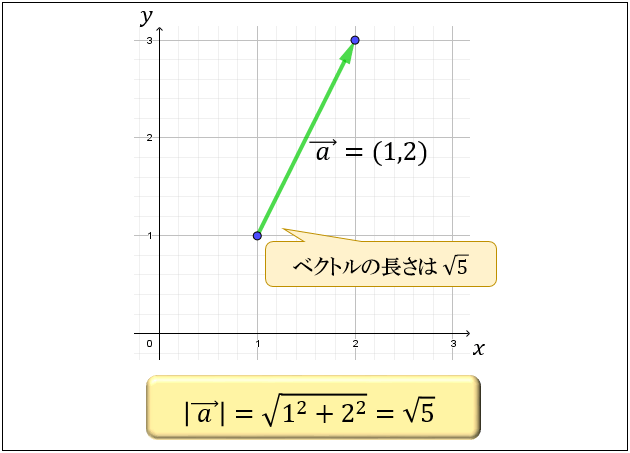
ベクトルとは何か その意味とベクトルの足し算 引き算 アタリマエ

ベクトルの成分を2乗するとベクトルの大きさの2乗になる というのが納 Yahoo 知恵袋

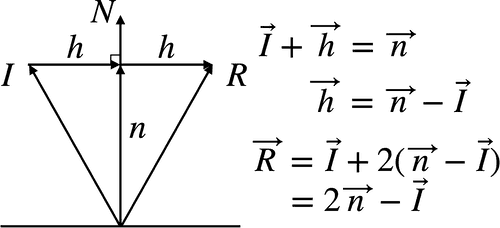
Glslのreflectとその計算方法 Yucchiy S Note

48s96ub7b0z5f Net Heimen Bekutoru Seibun

ベクトル編 高校のベクトルを基礎から復習 A 大学1年生もバッチリ分かる線形代数入門

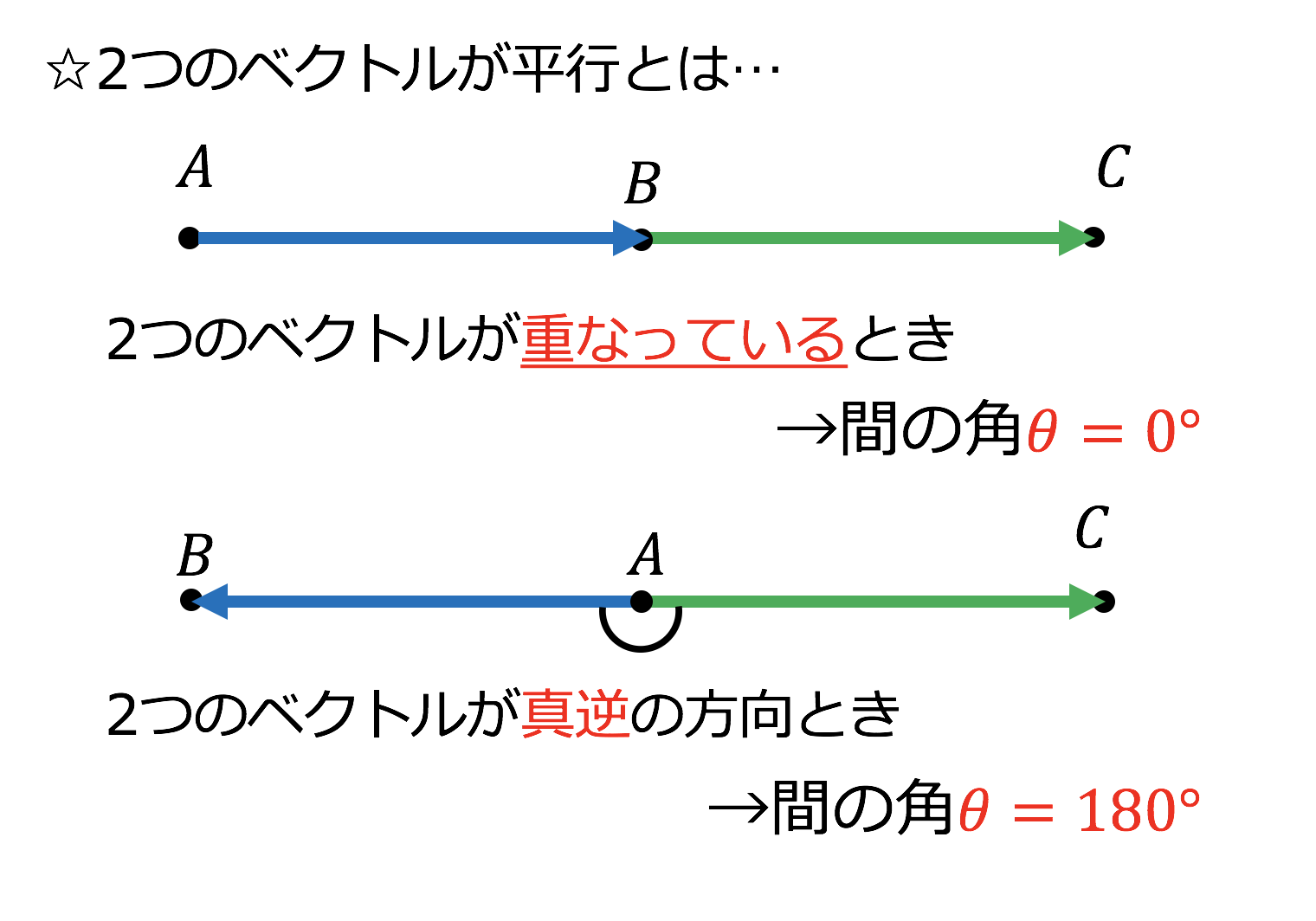
3分で分かる ベクトルの内積の2つの求め方 垂直 平行条件についてわかりやすく 合格サプリ

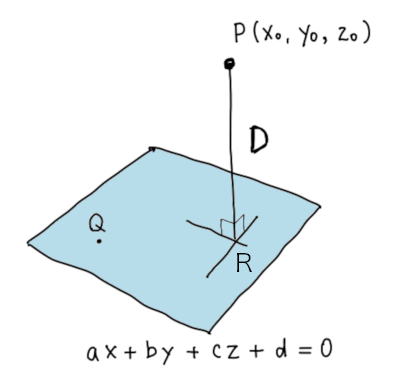
点と平面の距離 ベクトル解析 基礎からの数学入門

数学 内積ってなんぞ その２ 角度とｃｇ編 No More Retake

E Learnig Laboratory

06 幾何 17 ベクトルの内積や外積で3次元空間における面の向きを知りたい Flash Actionscript 3 0 Reference

高校数学b ベクトルの内積とax Byの最大最小 受験の月

ベクトルの大きさ 長さ を求める計算式と計算ツール Peko Step

ベクトル編 高校のベクトルを基礎から復習 A 大学1年生もバッチリ分かる線形代数入門

線形代数におけるベクトルの大きさと単位ベクトル 線形代数を宇宙一わかりやすく解説してみるサイト

ベクトル １５ 空間ベクトルの大きさ計算 怜悧玲瓏 高校数学を天空から俯瞰する

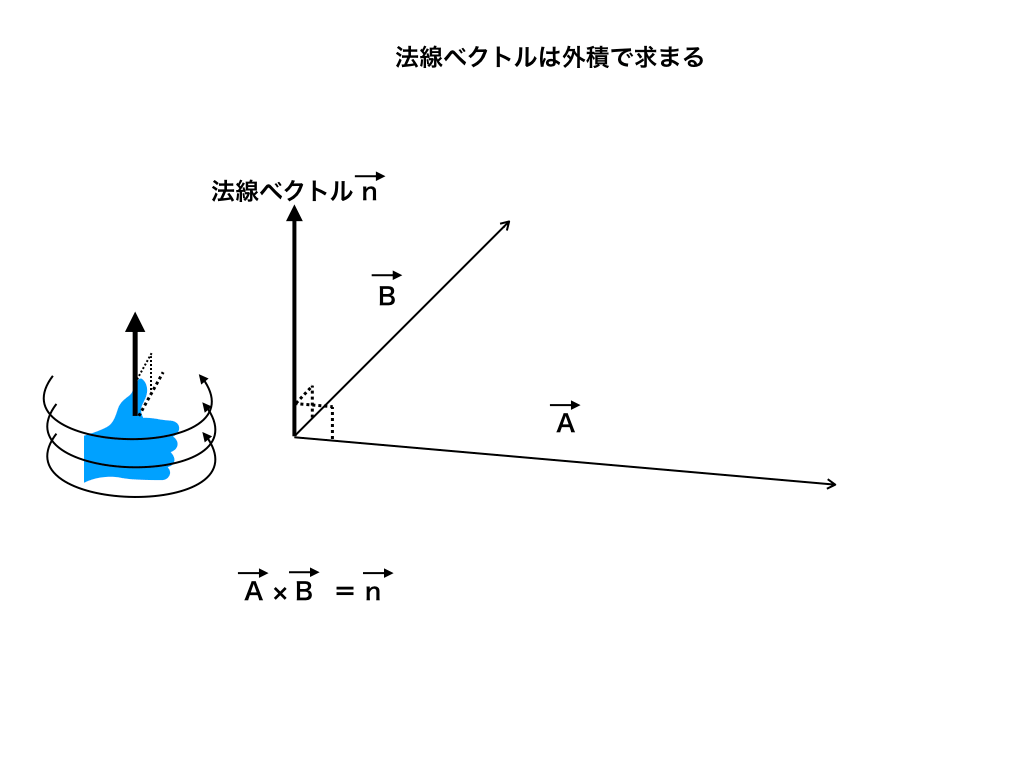
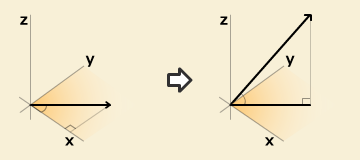
法線ベクトルの求め方と空間図形への応用

外積の計算のマイナス項の意味 直感的理解を目指して めもめもーめもblog

基礎の基礎編その１ 内積と外積の使い方

ベクトルの内積の全てを超わかりやすくまとめた 意味 公式 成分計算 理系ラボ

勉強しよう数学 ベクトルｐと単位ベクトルの内積はベクトルｐの単位ベクトルへの射影

ベクトルの表記法とベクトルの合成 やさしい電気回路

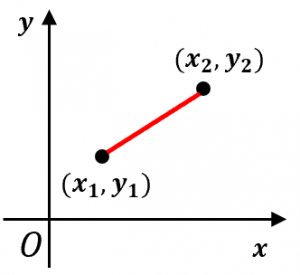
二点間の距離を求める公式 2次元 3次元 具体例で学ぶ数学

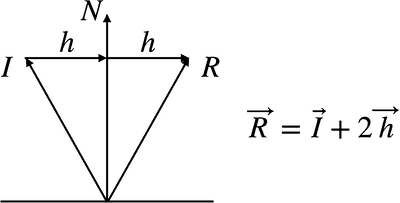
Glslのreflectとその計算方法 Yucchiy S Note

統計学や機械学習でもよく使われる相関係数が分かるベクトル計算の基礎知識 Ai エンジニアになるための 基礎数学 再入門 12 It

点と直線の距離公式をベクトルを使って導く すうがくブログ 式変形ch

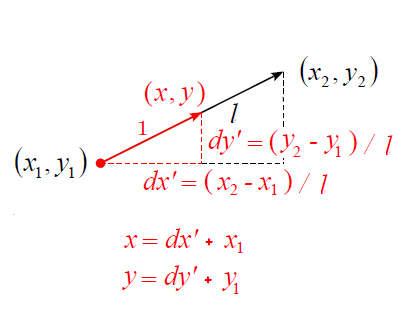
単位ベクトル ゆるゆるプログラミング

1

二乗平均速度と根二乗平均速度の公式と計算方法

基礎の基礎編その１ 内積と外積の使い方

ベクトルの内積とは何か 意味と使い方 高校数学の知識庫

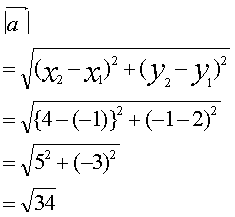
ベクトルの成分と大きさ

Pythonでベクトルの演算を行う方法を現役エンジニアが解説 初心者向け Techacademyマガジン

48s96ub7b0z5f Net Kuukan Bekutoru Gaiseki

ベクトル 高校物理の備忘録

48s96ub7b0z5f Net Kuukan Bekutoru Naiseki

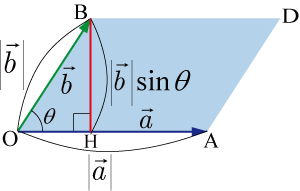
外積の大きさ

平面ベクトル問題 京極一樹の数学塾

Incoming Term: ベクトル 長さ 計算, ベクトル 長さ 計算機,