平方根のまとめのプリントです。 基本事項をしっかり確認してから取り組んでください。 →平方根の問題一覧 定期テスト対策、夏休みのまとめの学習、入試前の確認などにご利用ください。 練習問題をダウンロードする 画像をクリックす 16年6月7 整数部分、小数部分 学習はこちら: 平方根の小数部分と整数部分の問題|難易度別に解説 坂田先生 このジャンルの問題に初めてお目にかかる方のために、 ページの最初に基本の説明 を丁寧にしています。 にゃんこ 次のようなパターンの問題を第3学年 数学科学習指導案 1.単元名 「平方根」 2.単元について 私たちの生活の中には、黄金比や白銀比などのように、有理数だけでは表せない無理数が存在している。

中学数学 平方根 整数になる自然数n の簡単なやり方 丁寧な解説 スタディーランナップ
平方根の利用 指導案
平方根の利用 指導案- 平方根を利用した図形問題は様々にあります。 例えば、このような問題は平方根の記号に関する基本的な理解をつかわなければなりません。 一辺がxの正方形の面積が10のとき、xを求めよ。 このような問題の場合 2乗して10になる自然数は何ですか? 今回は平方根の利用問題を見ていく。 特に詰まりやすいところなので、ゆっくりとやっていこう。 前回←平方根の計算(標~難) 次回→平方根の利用(2)整数部分小数部分(標~難) 24 平方根の利用 241 整数・自然数になるようにする(標~難) 242 整数部分,小数部分(標~難)




2次方程式の解き方 平方完成を利用 数学fun
Z平方根の値を求める工夫 z平方根の加減 zいろいろな計算 *「ページ表示」を「見開き」でご覧いただきますと、問題とその 答えが見やすくなります。 *このテキストは家庭学習の補助教材としてのみご利用いただけま す。その他(問題の改変、商用など平方根応用 (図形) 図の ABCはAB=AC,∠BAC=90°の直角二等辺三角形である。 頂点Aから辺BCに垂線をおろしその交点をPとする。 AP=2cm, BC=4cmのとき次の問いに答えよ。 ABCの面積を求めよ。 辺ABの長さを求めよ。 平方根(ルート) 平方根の利用正方形の対角線、丸太、自然数を求める解き方は? いろんな利用問題を解説! kaztaro 中学数学・理科の学習まとめサイト! 平方根(ルート) ★有理化の仕方★やり方をまとめておくよ! 中学生 kaztaro
基本的に平方根は、このように+と-の数がセットで出てきます。 なので、これらをまとめて と表していくようになります。 (これをプラスマイナス2と読みます) それでは、例題をいくつか 9の平方根は ⇒ 25の平方根は ⇒ 81の平方根は ⇒ 平方根は22身のまわりにある平方根という観点から 221正方形 正方形には,JFが潜んでいるo対角線の長さである方眼紙を利用して面積が2,5,8,10の正 方形をかかせることから,JF,JF,Jg,Jiすの存在を知平方根(平方根の利用) 学年 組 氏名 直径㎝の丸太から,切り口ができるだけ大きな正方形になるように角材を切り出 したいと思います。次の問いに答えなさい。正方形の1辺の長さとその対角線の長さの 比は, であることは分かっています。
正の数の平方根の必要性と意味を理解し,正の数の平方根を含む簡単な式の計算ができるようにす るとともに,具体的な場面で平方根を表したり処理したりすることができるようにする。 教科名(数学) 第3学年 廿日市市立七尾中学校 広兼 孝明 単 元平方根の掘り下げ利用法 ・ とりあえず置く √ と log ① 平方根の大小 ② 有理数・無理数 ・ 有限小数になる分数の特徴 ・ 循環する無限を分数にする イ 数の平方根を含む式の計算 ① 有理化 ② 乗法・除法 ・ \(\small{\sqrt{a}}\) の形 ・ 平方根の近似値2次方程式 (平方根利用) 基礎 平方根の考え方 A 2 = 5 なら A = ± 5 この平方根の考え方を使って2次方程式を解く。 例題 x 2 = 16




中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Q Tbn And9gctlykh3qf568cm8iahl 3vpwv A8gvb7abdzhw0k2d7 4yumlhq Usqp Cau
「中3 数学 平方根の利用」 についてです。(問題)大きい円の中に,半径5cmの小さい円が4個ぴったりと入っている。その4個の円の中心は正方形の頂点になっている。(1)は分かったのですが、(2)が解説を見てもどうしても分かりません。解説が出平方根の覚え方 2、3、5などの平方根の値は暗記すると便利です。平方根の値は、物理学や工学で使うからです。語呂合わせを下記に示します。 上記の平方根は、最低限覚えるべきでしょう。 平方根の公式と問題 平方根の公式を下記に示します。平方根を利用した2次方程式の解き方 平方根を利用して解ける2次方程式の問題は次のようなものです。 x2 − 25 = 0 x 2 − 25 = 0 2x2 − 16 = 0 2 x 2 − 16 = 0 (x 1)2 = 25 ( x 1) 2 = 25 「 x2 x 2 の項」と「定数」だけからなる2次方程式、または「 x x の1次式の2乗」と



Laf先生 正方形の対角線の求め方 中3数学 平方根の利用 Powered By Line




平方根 掛け算のやり方をサクッと解説 中学数学 理科の学習まとめサイト
3 多項式(3) ~式の計算の利用~ ホップ ステップ ジャンプ 4 平方根(1) ~平方根~ ホップ ステップ ジャンプ 5 平方根(2) ~素因数分解~ ホップ ステップ 6 平方根(3) ~根号をふくむ式の計算~ ホップ ステップ ジャンプ 7 2次方程式(1) 標本調査の活用 高校入試問題 学習プリント 中間・期末テスト 前ちゃんの中学校数学の部屋:自宅学習(生徒向け) 3年 平方根の利用 ねらい「 平方根を具体的な場面で利用すること・平方根の近似値の求め方を考える。 ・有理数と無理数の意味を理解して いる。 ノート 5 数を素因数分解することができる。 ・数を素因数分解する。 ・素因数分解を利用して、平方根を 求めたり、平方因数をみつけたりす ることができる。



Sukinakazu Net Heihoukonn Heihoukonn Pdf
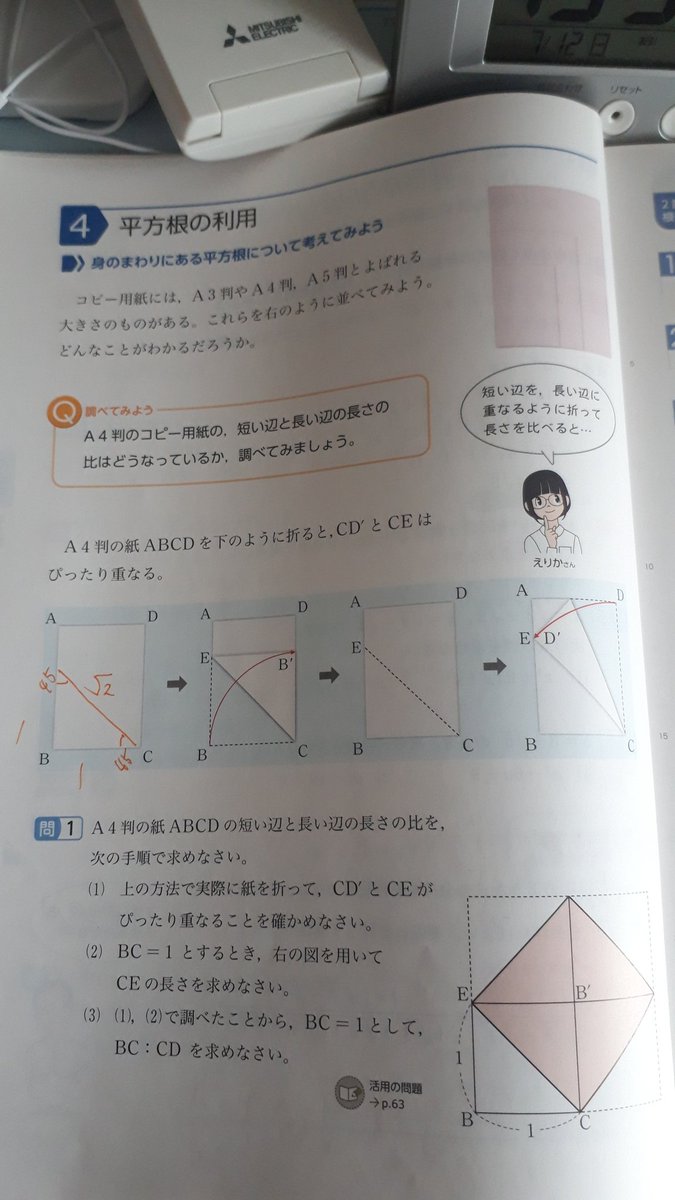



平方根
平方根を利用した解き方 2次方程式 2次方程式の計算でよく使うのは因数分解を利用した方法ですが、この平方根を利用する方法は忘れられやすいです。 ですが、覚えておけばこちらのほうが早くて簡単に計算できるケースは意外と多いです。14 身のまわりで,平方根が利用さ ・身のまわりの平方根に関心をもち,平方根が利用されている具体 れている場面について考える。 的な場面を調べたり,そのよさを考えたりしようとしている。 今回は、前回に引き続き平方根の利用の問題です。 高校生になっても触れる内容なので、今のうちに出来るように。 前回←平方根の利用(1)(整数になるようなn)(標~難) 次回→平方根の利用(3)(範囲を満たす平方根)(標~難)




平方根の利用なのですが 解説を読んでも理解できませんでした どなたか教えてください Clear




平方根の利用 ルートの中の自然数nを求める問題一覧 坂田先生のブログ
キーンコーンカーンコーン♪ 6月14日(日) 朝の会始めまーす。 今日は、「平方根で、人気は左右される」という話をしまーす。 今から、平方根の説明をします。めちゃくちゃつまらないので、説明の部分はとばしてもらってもいいです。 まず、数には有理数と無理数があります。 有理数③ 根号を用いて平方根を表したり,平方根を含む式の四則計算をしたりすることができる。 ④ 平方根の必要性と意味,四則計算の方法などを理解することができる。 3 単元の評価規準 数学への関心・意欲・態度 数学的な見方や考え方平方根① 平方根を求める(整数) 平方根を求める(小数) 平方根を求める(分数) 平方根を求める(整数2) 平方根を求める(整数3) 1~99の平方根;




中学数学 平方根の利用 ママ塾ノート




平方根の利用 中3数学 平方根9 Youtube
平方根の利用③ 中学3年 数学 平方根の利用③ 問題はこちらです。 問題 直径が30cmの丸太から、切り口ができるだけ大きな正方形となるように角材をとる。 このとき次の問いに答えよ。 (1)正方形の面積を求めよ。 (2)正方形の1辺を根号を用いて第3学年2章平方根「平方根の利用」の指導案(略案) 北海道教育大学附属釧路中学校 赤本 純基 ・本時の目標 数の平方根を活用して,問題の解決の仕方を説明できる。(思考・判断・表現) ・本時の展開中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード・印刷 中学3年生 数学 平方根の加法・減法 問題プリント 無料ダウンロード・印刷 中学3年生 数学 平方根の乗法・除法 問題プリント 無料ダウンロード・印刷




人気の 平方根 動画 35本 ニコニコ動画




平方根 18aの平方根が自然数となるようなaの求め方 中学生からの勉強質問 数学 進研ゼミ中学講座
平方根 (利用②) 中3数学 定期テストや実力テストに出題されやすい問題です。 ルートの中に2乗のものを残すことがポイントです。 そのためには素因数分解が必須ですよ。16の平方根は、±4 25の平方根は、±5 とすぐ答えることができます。 「平方根は、いつも2つある」 ことを、 忘れないでくださいね! 「2乗になる数」がない?? では、ここから先が「ルート」の話です。 いきなり質問から。 「3の平方根は?- 中学3年「平方根」の実践から 一 1 単元のねらい (1) 正の数の平方根の必要性と意味を理解し,正の数の平方根を含む簡単な式の計算ができる ようにするとともに,具体的な場面で平方根を用いて表したり処理したりすることができ るようにする。




中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ




中3数学 2次方程式の解き方 平方根の利用 Youtube
平方根の加減 3 +2 を例に考える。 まず をaとおくと、 3 +2 =3a+2a=5a ここでaに をもどすと、答えは5 になる。 したがって平方根の加減では、根号の中身は変えずに、根号の外側だけを計算する。 平方根は文字式と同様の考え方で計算できる。平方根の意味を理解して いる。 3 している。 正方形の1 辺の長さを比 べて,平方根の大小を考 えることができる。 平方根の大小を,不等 号を使って表すことがで きる。 平方根の大小関係を理解 4 これまで学んだ数を有 理数と無理数に分類で きる。数学教育 07年2月号/平方根の利用 身近にある平方根こんなところに√2や√3が 詳細情報 特集 新しい数としての「平方根」 平方根の利用 身近にある平方根こんなところに√2や√3が 書誌 数学教育 07年2月号




平方根の利用 1 整数 自然数になるようなn 標 難 数学の解説と練習問題



Www Pref Oita Jp Uploaded Attachment Pdf



Http Www Ogori Mii Ed Jp Ohara J Hp 10 0kennkyuu 19knenkyuu31 05suugaku Pdf



Http Www E Shiroi Jp Center Sidoan Tyu 3 E5 B9 B4 E6 95 B0 E5 Ad A6 E5 B9 E6 96 B9 E6 A0 B92 Pdf



Q Tbn And9gcral90caflwd9iqwoqpidvoqmwx erlihf79qizyo1ho6619z Usqp Cau




二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学




中3 数学 平方根の利用 この問題の解説をお願いします 整数部分と少数 Okwave




メルカリ 中3 数学 コンプリート Lead 臨海セミナー 参考書 800 中古や未使用のフリマ




中3数学 平方根の利用 Youtube




P65 Lihat Cara Penyelesaian Di Qanda




広陵ブログver 2 数学の研究授業



平方根の利用です直径5cmの円があります この円の中に直径2c Yahoo 知恵袋




数学 質問解答 平方根の利用 の わかりやすい 考え方 解き方はこちらです 文章題 平方根 中3 中学数学 質問ありがとうございました 行間 ぎょうのあいだ 先生



2次方程式の解き方 平方根を利用 数学fun




中3数学 平方根を利用した問題 勉強 Youtube スタディチューブ




中学校数学自宅学習3年 平方根の最初




平方根や二次関数って社会で何の役に立つの 大人が使う場面とは ミラブロ




中学3年生 数学 平方根の利用 文章題 6月11日金曜日 Youtube




3 平方根を利用した解き方 Mathweather4067のblog



Www Kenshinkan Jr Com School Summer Pdf Daikyofozokuclass21 Pdf




D60 Lihat Cara Penyelesaian Di Qanda




平方根の利用 清水塾




中3 数学 平方根の利用 についてです 方眼の1目盛りは1cmで 四角 数学 教えて Goo




平面図形37 平方根の作図 怜悧玲瓏 高校数学を天空から俯瞰する




平方根




二次方程式の解き方 平方根を利用 チーム エン




平方根の応用 無料で使える中学学習プリント




中学数学 平方根 整数になる自然数n の簡単なやり方 丁寧な解説 スタディーランナップ




8 3 Sqrta4 Bardfrac 5 5 Descubre Como Resolverlo En Qanda




平方根の式の値 無料で使える中学学習プリント




平方根の利用 2 整数部分小数部分 標 難 数学の解説と練習問題




平方根の利用 清水塾



中3数学 平方根の利用についての問題です 意味が分かるよう Yahoo 知恵袋



数学的活動を支援する動画01 平方根 分母の有理化



練馬区立開進第三中学校



中学3年平方根の利用問題です この解き方を教えてください ふつうに Yahoo 知恵袋



Http Kylaboratory Com Wp Wp Content Uploads 19 03 67ede58ac547ffb2fa9ce99b7caf 1 Pdf




中3数学2 19 平方根の利用 代入編 Youtube




平方根の利用で丸太の問題について質問です 面積の求め方はわかった 中学校 教えて Goo




最も選択された 平方根 の 利用 問題 ニスヌーピー 壁紙




中学3年生 数学 平方根 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




平方根の利用 清水塾




平方根を利用した解き方 ドリるーむ



数学教育 07年2月号 平方根の利用 身近にある平方根 こんなところに 2や 3が



Q Tbn And9gct9hhlres3mgnxsawubvt3s T9sg2pd Doyk4hnfwqd74euivdg Usqp Cau




平方根の利用の部分です 解説お願いします Clear



Www Edu Ctr Pref Nagano Lg Jp Kjouhou Manabi Hiroba 05 Review Mondai Mondai S Re Chu3 02 31 Pdf




平方根の利用の対角線を求める問題について詳しく説明お願いします Clear




中学数学 平方根の利用 ママ塾ノート




平方根の利用 正方形の対角線 丸太 自然数を求める解き方は いろんな利用問題を解説 中学数学 理科の学習まとめサイト
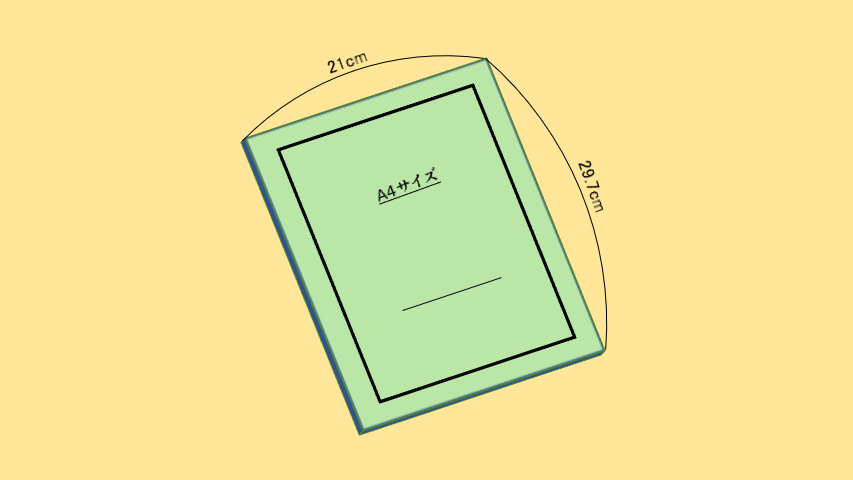



生活に役立つ数学 平方根 ルート2 ふみの会社経営日記



Mondaibank Jimdofree Com App Download Ef 93 E5 B9 B4 Ef 92 E7 Ab A0 E5 B9 E6 96 B9 E6 A0 B9 80 8c E5 B9 E6 96 B9 E6 A0 B9 81 Ae E5 E7 94 A8 80 8d Pdf T




2次方程式の解き方 平方完成を利用 数学fun




二次方程式の解と平方根を利用した解き方 無料で使える中学学習プリント



Http Ncsaas Cu Mo Jp Ehime Htdocs E6 8c 87 E5 B0 8e 81 Ab E5 B9 E7 Ab 8b 81 E6 85 E5 A0 B1 E5 B9 E6 9029 E5 B9 B4 E5 Ba A6 E7 A0 94 E7 B6 E8 87 E6 96 99 E5 E4 9a E6 8c 87 E5 B0 8e E6 A1 Action Common Download Main Upload Id 46




中学数学 平方根の利用 ママ塾ノート




二次方程式 平方完成 チーム エン




平方根の利用 ルートのついた数が整数となる問題を わかりやすく解説 中学数学




中3 数学 平方根の利用 についてです 問題 大きい円の中に 半径5c 数学 教えて Goo




すうがくラボのブログ 18




数学の勉強のコツ 中3平方根編 学習塾コンパス 学習塾compass



2次方程式 平方根の考え方を利用した解法 その2 すうがくラボのブログ




中学数学3年 2次方程式 平方根の利用 受験の月



2




中3 平方根の利用 この問題の解き方を教えてください Clear




2 4cm 6cm0 Lihat Cara Penyelesaian Di Qanda



中学3年の平方根の利用です 2の作図についてですが 模範解答 Yahoo 知恵袋



2




二次方程式 平方根の考えを使った解き方 平方完成を利用した解き方を解説 数スタ




たくさん質問すみません この問題も解説をよろしくお願いいたします Clear




お絵かきできるかな 中3数学 平方根の利用 赤城 ᐡᐤᐡ




この問題を教えていただきたいです Clear
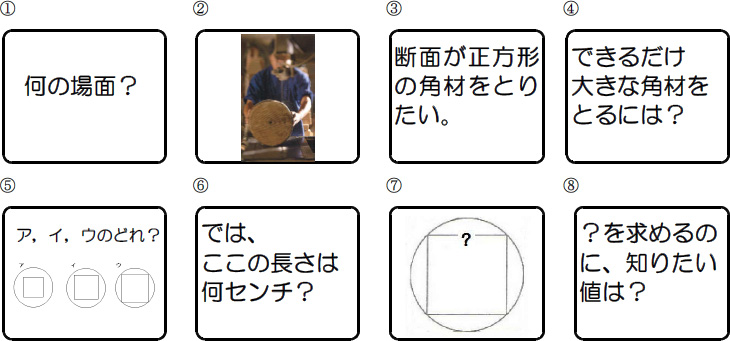



主体的 対話的で深い学び の実現に向けた授業改善の工夫 第3学年 平方根の利用 の実践を通して 授業実践記録 アーカイブ一覧 授業支援 サポート資料 数学 中学校 知が啓く 教科書の啓林館




正方形の対角線の求め方 中3数学 平方根の利用 Youtube



Mondaibank Jimdofree Com App Download Ef 93 E5 B9 B4 Ef 92 E7 Ab A0 E5 B9 E6 96 B9 E6 A0 B9 80 8c E5 B9 E6 96 B9 E6 A0 B9 81 Ae E5 E7 94 A8 80 8d Pdf T



2




Youtube Lesson 中3 平方根 第8回 利用 を自然数にするn 桂坂数学教室
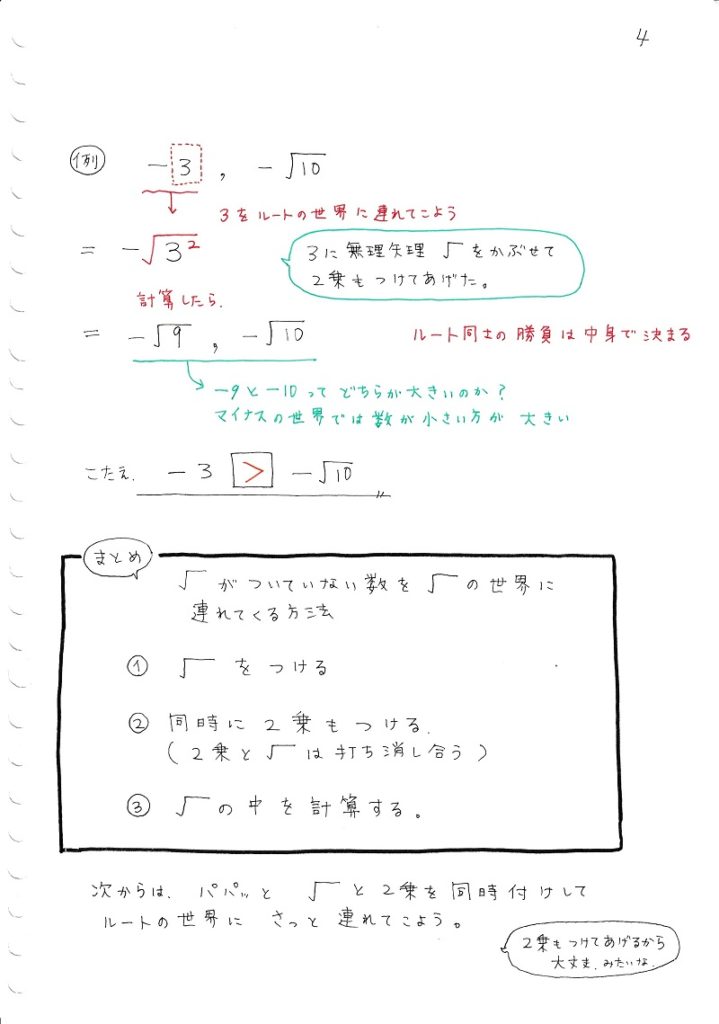



中学数学 平方根 ママ塾ノート



Http Www Edu C Pref Miyagi Jp Midori Gakuryoku Plan Pdf A Pdf 9nen A 9 02 Pdf




中3 数学 平方根問題 応用 慣れれば無双も夢じゃない 授業動画あり アオイのホームルーム



至急 中3数学平方根の利用です 途中計算が画像のようになる理由 Yahoo 知恵袋




二次方程式の解き方 ねらい 二次方程式を 平方根を利用して解くことができる 本時の流れ 前時の復習でax2 bの解き方を確認する Ppt Download



Http Www Shimane Fuzoku Ed Jp Wp Wp Content Uploads 17 03 12 C3 Sugaku Pdf




Sqrt45 N1 N Descubre Como Resolverlo En Qanda



Http Www Edu C Pref Miyagi Jp Midori Gakuryoku Plan Pdf M Pdf 9nen M 9 02 Pdf




2次方程式 1 解き方 因数分解 平方根 平方完成 解の公式 バカでもわかる 中学数学




年度用 中学校数学教科書内容解説資料 未来へひろがる数学




ベストコレクション 平方根 の 利用 平方根の利用 問題集 Nyosspixm3db



1




中3の数学の平方根の利用です 解き方がわからないです Clear



0 件のコメント:
コメントを投稿